Smalltalk80LanguageImplementation:Chapter 11
- Chapter 11 Three Examples that Use Collections
Three Examples that Use Collections
Three examples of class descriptions are given in this chapter. Each example makes use of the numeric and collections objects available in the Smalltalk-80 system; each illustrates a different way to add functionality to the system.
Card games can be created in terms of random selection from a collection representing a deck of cards. The example class Card represents a playing card with a particular suit and rank. CardDeck represents a collection of such Cards; a CardHand is a collection of Cards for an individual player. Selecting cards from a CardDeck or a CardHand is carried out using example classes that represent sampling with replacement, SampleSpaceWithReplacement, and sampling without replacement, SampleSpaceWithoutReplacement. A well-known programming problem, the drunken cockroach problem, involves counting the number of steps it takes a cockroach to randomly travel over all the tiles in a room. The solution given in this chapter represents each tile as an instance of example class Tile and the bug as an instance of DrunkenCockroach. The third example in this chapter is of a tree-like data structure represented by classes Tree and Node; a WordNode illustrates the way trees can be used to store strings representing words.
Random Selection and Playing Cards
The Smalltalk-80 class Random, which acts as a generator for randomly selected numbers between 0 and 1, was described in Chapter 8. Random provides the basis for sampling from a set of possible events; such a set is known as a sample space. A simple form of discrete random sampling can be obtained in which a random number is used to to select an element from a sequenceable collection. If the selected element remains in the collection, then the sampling is done "with replacement"--that is, every element of the collection is available each time the collection is sampled. Alternatively, the sampled element can be removed from the collection each time the collection is sampled; this is sampling "without replacement."
Class SampleSpaceWithReplacement represents random selection with replacement from a sequenceable collection of items. An instance of the class is created by specifying the collection of items from which random sampling will be done. This initialization message has selector data:. We then sample from the collection by sending the instance the message next. Or we can obtain anInteger number of samples by sending the message next: anInteger.
For example, suppose we wish to sample from an Array of Symbols representing the names of people.
people ← SampleSpaceWithReplacement
data: #(sally sam sue sarah steve)
Each time we wish to select a name from the Array, we evaluate the expression
people next
The response is one of the Symbols, sally, sam, sue, sarah, or steve. By evaluating the expression
people next: 5
an OrderedCollection of five samples is selected. Instances of SampleSpaceWithReplacement respond to messages isEmpty and size to test whether any elements exist in the sample space and how many elements exist. Thus the response to
people isEmpty
is false; and the response to
people size
is 5.
An implementation of class SampleSpaceWithReplacement is given next. Comments, delimited by double quotes, are given in each method to indicate its purpose.
| class name | SampleSpaceWithReplacement |
| superclass | Object |
| instance variable names | data rand |
| class methods | instance creation
data: aSequenceableCollection
"Create an instance of SampleSpaceWithReplacement such that the argument, aSequenceableCollection, is the sample space."
↑self new setData: aSequenceableCollection
|
| instance methods | accessing
next
"The next element selected is chosen at random from the data collection. The index into the data collection is determined by obtaining a random number between 0 and 1, and normalizing it to be within the range of the size of the data collection."
self isEmpty
ifTrue: [self error: 'no values exist in the sample space'].
↑data at: (rand next * data size) truncated + 1
next: anInteger
"Answer an OrderedCollection containing anInteger number of selections from the data collection."
| aCollection |
aCollection ← OrderedCollection new: anInteger.
anInteger timesRepeat: [aCollection addLast: self next].
↑aCollection
testing
isEmpty
"Answer whether any items remain to be sampled."
↑self size = 0
size
"Answer the number of items remaining to be sampled."
↑data size
private
setData: aSequenceableCollection
"The argument, aSequenceableCollection, is the sample space, Create a random number generator for sampling from the space."
data ← aSequenceableCollection.
rand ← Random new
|
The class description declares that each instance has two variables whose names are data and rand. The initialization message, data:, sends the new instance the message setData: in which data is bound to a SequenceableCollection (the value of the argument of the initialization message) and rand is bound to a new instance of class Random.
SampleSpaceWithReplacement is not a subclass of Collection because it implements only a small subset of the messages to which Collections can respond. In response to the messages next and size to a SampleSpaceWithReplacement, the messages at: and size are sent to the instance variable data. This means that any collection that can respond to at: and size can serve as the data from which elements are sampled. All SequenceableCollections respond to these two messages. So, for example, in addition to an Array as illustrated earlier, the data can be an Interval. Suppose we wish to simulate the throw of a die. Then the elements of the sample space are the positive integers 1 through 6.
die ← SampleSpaceWithReplacement data: (1 to: 6)
A throw of the die is obtained by evaluating
die next
The response from this message is one of the Integers, 1, 2, 3, 4, 5, or 6.
We could select a card from a deck of cards in a similar way if the collection associated with the instance of SampleSpaceWithReplacement consists of elements representing playing cards. In order to play card games, however, we have to be able to deal a card out to a player and remove it from the deck. So, we have to use random selection without replacement.
To implement random selection without replacement, we define the response to the message next as removing the selected element. Since all SequenceableCollections do not respond to the message remove:, (for example, Interval does not) we either must check the argument of the initialization message or we must convert the argument to an acceptable kind of collection. Since all OrderedCollections respond to the two messages, and since all collections can be converted to an OrderedCollection, we can use the conversion approach. The method associated with setData: sends its argument the message asOrderedCollection in order to accomplish the goal.
Class SampleSpaceWithoutReplacement is defined to be a subclass of SampleSpaceWithReplacement. The methods associated with the messages next and setData: are overridden; the remaining messages are inherited without modification.
| class name | SampleSpaceWithoutReplacement |
| superclass | SampleSpaceWithReplacement |
| instance methods | accessing
next
↑data remove: super next
private
setData: aCollection
data ← aCollection asOrderedCollection.
rand ← Random new
|
Notice that the method for next depends on the method implemented in the superclass (super next). The superclass's method checks to make certain that the sample space is not empty and then randomly selects an element. After determining the selected element, the subclass's method removes the element from data. The result of the remove: message is the argument, so that the result of the message next to a SampleSpaceWithoutReplacement is the selected element.
Now let's implement a simple card game. Suppose the sample space data for the card game are instances of a class Card where each Card knows its suit and rank. An instance of Card is created by sending it the message suit:rank:, specifying the suit (heart, club, spade, or diamond) and its rank (1, 2, ..., 13) as the two arguments. A Card responds to the messages suit and rank with the appropriate information.
| class name | Card |
| superclass | Object |
| instance variable names | suit rank |
| class methods | instance creation
suit: aSymbol rank: anInteger
"Create an instance of Card whose suit is the argument, aSymbol, and whose rank is the argument, anInteger."
↑self new setSuit: aSymbol rank: anInteger
|
| instance methods | accessing
suit
"Answer the receiver's suit."
↑suit
rank
"Answer the receiver's rank."
↑rank
private
setSuit: aSymbol rank: anInteger
suit ← aSymbol.
rank ← anInteger
|
A deck of cards, cardDeck, is created by the following expressions.
cardDeck ← OrderedCollection new: 52.
#(heart club spade diamond) do:
[ :eachSuit |
1 to: 13 do: [ :n | cardDeck add: (Card suit: eachSuit rank: n)]]
The first expression creates an OrderedCollection for 52 elements. The second expression is an enumeration of the ranks 1 through 13 for each of the four suits: heart, club, spade, and diamond. Each element of the OrderedCollection is set to be a Card with a different suit and rank.
The ability to sample from this deck of cards is obtained by creating an instance of SampleSpaceWithoutReplacement with the card deck as the collection from which samples will be taken
cards ← SampleSpaceWithoutReplacement data: cardDeck
To deal a card, evaluate the expression
cards next
The response to this message is an instance of class Card.
Another way to provide a deck of playing cards is illustrated in the description of example class CardDeck. The basic idea is to store a linear list of cards; next means supply the first card in the list. A card can be returned to the deck by placing it at the end or by inserting it at some random position. The linear list is made random by shuffling-that is, randomly ordering the cards.
In the implementation of class CardDeck provided next, we store an initial version of the deck of cards as a class variable. It is created using the expressions given earlier. A copy of this variable is made as an instance variable whenever a new instance is created; it is shuffled before cards are dealt out. Each subsequent shuffle of the deck uses the current state of the instance variable, not of the class variable. Of course, the shuffling process, since it is based on the use of an instance of SampleSpaceWithoutReplacement, is quite uniform. A simulation of real shuffling involves first splitting the deck approximately in half and then interleaving the two halves. The interleaving involves selecting chunks from one half and then the other half. Indeed, such a simulation may be more random than an actual person's shuffling; a person's shuffling ability might be observable and predictable.
Messages to a CardDeck, such as return:, next, and shuffle, are useful in creating card games.
| class name | CardDeck |
| superclass | Object |
| instance variable names | cards |
| class variable names | InitialCardDeck |
| class methods | class initialization
initialize
"Create a deck of 52 playing cards."
InitialCardDeck ← OrderedCollection new: 52.
#(heart club spade diamond) do:
[ :aSuit |
1 to: 13
do: [ :n | InitialCardDeck add: (Card suit: aSuit rank: n)]]
instance creation
new
"Create an instance of CardDeck with an initial deck of 52 playing cards."
↑super new cards: InitialCardDeck copy
|
| instance methods | accessing
next
"Deal (give out) the next card."
↑cards removeFirst
return: aCard
"Put the argument, aCard, at the bottom of the deck."
cards addLast: aCard
shuffle
| sample tempDeck |
sample ← SampleSpaceWithoutReplacement data: cards.
tempDeck ← OrderedCollection new: cards size.
cards size timesRepeat: [tempDeck addLast: sample next].
self cards: tempDeck
testing
isEmpty
"Answer whether any more cards remain in the deck."
↑cards isEmpty
private
cards: aCollection
cards ← aCollection
|
The class CardDeck must be initialized by evaluating the expression
CardDeck initialize
In the implementation of CardDeck, cards is the instance variable and is therefore the deck of cards used in playing a game. To play a game, an instance of CardDeck is created
CardDeck new
and then each card is dealt by sending this new instance the message next. When a card is put back in the deck, the CardDeck is sent the message return:. Shuffling always shuffles whichever cards are currently in the deck. If a full CardDeck is to be reused after a round of play, any cards taken from the deck must be returned.
Note the implementation of the message shuffle. A sample space without replacement, sample, is created for a copy of the current deck of cards. A new OrderedCollection, tempDeck, is created for storing randomly selected cards from this sample space. Sampling is done from sample for each possible card; each selected card is added to the tempDeck. Once all the available cards have been shuffled into it, tempDeck is stored as the current game deck.
Suppose we create a simple card game in which there are four players and a dealer. The dealer deals out cards to each of the players. If at least one of the players has between 18 and 21 points, the game ends with the "prize" divided among each of these players. Points are counted by adding up the ranks of the cards. A player with more than 21 points is not dealt new cards.
Each player is represented by an instance of class CardHand that represents a card hand. A CardHand knows the cards it is dealt and can determine its total point count (in response to the message points).
| class name | CardHand |
| superclass | Object |
| instance variable names | cards |
| class methods | instance creation
new
↑super new setCards
|
| instance methods | accessing
take: aCard
"The argument, aCard, is added to the reciever."
cards add: aCard
returnAllCardsTo: cardDeck
"Place all of the receiver's cards into the deck of cards referred to by the argument, cardDeck, and remove these cards from the receiver's hand."
cards do: [ :eachCard | cardDeck return: eachCard].
self setCards
inquiries
points
"Answer the sum of the ranks of the receiver's cards."
↑cards inject: 0 into: [ :value :nextCard | value + nextCard rank]
private
setCards
cards ← OrderedCollection new
|
We create a Set of four players. Each player is represented by an instance of CardHand. The dealer's cards are the gameCards. The dealer (that is, the programmer) starts by shuffling the deck; there is no winner yet. There may be more than one winner; winners will be listed in the Set, winners.
players ← Set new.
4 timesRepeat: [players add: CardHand new].
gameCards ← CardDeck new.
gameCards shuffle
As long as there is no winner, each player with less than 21 points is given another card from the gameCards. Before dealing a card to each eligible player, the dealer looks to see if there are any winners by testing the points for each player.
[ winners ← players select: [ :each | each points between: 18 and: 21].
winners isEmpty and: [gameCards isEmpty not]]
whileTrue:
[players do:
[ :each |
each points < 21 ifTrue: [each take: gameCards next]
The condition for continuing to play is a block with two expressions. The first expression determines the winners, if any, The second expression tests to see if there are any winners yet (winners isEmpty) and, if not, if there are any more cards to deal out (gameCards isEmpty not). If there are no winners and more cards, the game continues. The game consists of an enumeration of each player; each player takes another card (each take: gameCards next)only if the number of card points is less than 21 (each points < 21).
To play again, all cards have to be returned to the game deck, which is then shuffled.
players do: [ :each | each returnAllCardsTo: gameCards].
gameCards shuffle
The players and dealer are ready to play again.
The Drunken Cockroach Problem
We can use some of the collection classes to solve a well-known programming problem. The problem is to measure how long it takes a drunken cockroach to touch each tile of a floor of square tiles which is N tiles wide and M tiles long. To slightly idealize the problem: in a given "step" the cockroach is equally likely to try to move to any of nine tiles, namely the tile the roach is on before the step and the tiles immediately surrounding it. The cockroach's success in moving to some of these tiles will be limited, of course, if the cockroach is next to a wall of the room. The problem is restated as counting the number of steps it takes the cockroach to land on all of the tiles at least once.
One straightforward algorithm to use to solve this problem starts with an empty Set and a counter set to 0. After each step, we add to the Set the tile that the cockroach lands on and increment a counter of the number of steps. Since no duplication is allowed in a Set, we would be done when the number of elements in the Set reaches N*M. The solution would be the value of the counter.
While this solves the simplest version of the problem, we might also like to know some additional information, such as how many times each tile was visited. To record this information, we can use an instance of class Bag. The size of the Bag is the total number of steps the cockroach took; the size of the Bag when it is converted to a Set is the total number of distinct tiles touched by the cockroach. When this number reaches N*M, the problem is solved. The number of occurrences of each tile in the Bag is the same as the number of times the roach visited each tile.
Each tile on the floor can be labeled with respect to its row and its column. The objects representing tiles in the solution we offer are instances of class Tile. A commented implementation of class Tile follows.
| class name | Tile |
| superclass | Object |
| instance variable names | location floorArea |
| instance methods | accessing
location
"Answer the location of the receiver on the floor."
↑location
location: aPoint
"Answer the location of the receiver on the floor."
↑location
location: aPoint
"Set the receiver's location on the floor to be the argument, aPoint."
location ← aPoint
floorArea: aRectangle
"Set the floor area to be the rectangular area represented by the argument, aRectangle."
floorArea ← aRectangle
moving
neighborAt: deltaPoint
"Create and answer a new Tile that is at the location of the receiver changed by the x and y amounts represented by the argument, deltaPoint. Keep the location of the newTile within the boundries of the floor area."
| newTile |
newTile ← Tile new floorArea: floorArea.
newTile location: ((location + deltaPoint max: floorArea origin)
min: floorArea corner).
↑newTile
comparing
= aTile
"Answer whether the receiver is equal to the argument, aTile."
↑(aTile isKindOf: Tile) and: [location = aTile location]
hash
↑location hash
|
A Tile refers to its row and column locations, each of which must be at least 1 and no larger than the width or length of the floor. Therefore, in addition to remembering its location, a Tile must remember the maximum floor space in which it can be placed. A Tile can be sent the message neighborAt: aPoint in order to determine a Tile at one of the locations next to it. This new Tile must be at a location within the boundaries of the floor.
The way we will simulate the cockroach's walk is to select a direction in terms of changes in the x-y coordinates of the cockroach's location. Given the location of the cockroach (tile x,y), there are 9 tiles to which the insect can move unless the tile is along one of the edges. We will store the possible changes of x and y in an OrderedCollection that is the data for random selection. The OrderedCollection will contain Points as elements; the Points are direction vectors representing all the possible combinations of moves. We create this collection by the expressions
Directions ← OrderedCollection new: 9.
(-1 to: 1) do: [ :x | (-1 to: 1) do: [ :y | Directions add: x@y]]
Directions, then, is a collection with elements
-1@-1, -1@0, -1@1, 0@-1, 0@0, 0@1, 1@-1, 1@0, 1@1
As part of the drunken walk simulation, we will generate a random number for selecting an element from this OrderedCollection of possible moves. As an alternative to using a random number generator directly, we could use the previous example's SampleSpaceWithReplacement with Directions as the sample space.
Suppose the cockroach starts on the Tile that is at location 1®1. Each time the cockroach is supposed to take a step, we obtain an element from the collection, Directions. This element is then the argument of the message neighborAt: to the Tile. In the following, assume Rand is an instance of class Random.
tile neighborAt:
(Directions at: ((Rand next * Directions size) truncated + 1)).
The resulting new tile location is the place where the cockroach landed.
Each tile position has to be remembered in order to be able to report on whether every location has been touched and how many steps were required. By storing each tile in a Bag, a tally is kept of the number of times the cockroach landed in each location. So at each step, a new tile is created that is a copy of the previous tile. This new tile is changed according to the randomly selected direction and is added to the Bag. When the number of unique elements of the Bag equals the total number of tiles, the cockroach is done.
Only two messages are needed in class DrunkenCockroach. One is a command to have the cockroach take a walk around a specific floor area until every tile on the floor has been touched. This is the message walkWithin:startingAt:. The second is an inquiry as to the number of steps the cockroach has taken so far; this is the message numberOfSteps. We can also inquire about the number of times the roach stepped on a particular tile by sending the DrunkenCockroach the message timesSteppedOn:. The collection of direction vectors (as described earlier) is created as a class variable of DrunkenCockroach; the random number generator Rand is also a class variable of DrunkenCockroach.
| class name | DrunkenCockroach |
| superclass | Object |
| instance variable names | currentTile tilesVisited |
| class variable names | Directions Rand |
| class methods | class initialization
initialize
"Create the collection of direction vectors and the random number generator."
Directions ← OrderedCollection new: 9.
(-1 to: 1) do: [ :x | (-1 to: 1) do: [ :y | Directions add: x@y]].
Rand ← Random new
instance creation
new
↑super new setVariables
|
| instance methods | simulation
walkWithin: aRectangle startingAt: aPoint
| numberTiles |
tilesVisited ← Bag new.
currentTile location: aPoint.
currentTile floorArea: aRectangle.
numberTiles ← (aRectangle width + 1) * (aRectangle height + 1).
tilesVisited add: currentTile.
[tilesVisited asSet size < numberTiles] whileTrue:
[currentTile ← currentTile neighborAt:
(Directions at: (Rand next * Directions size) truncated + 1).
tilesVisited add: currentTile]
data
numberOfSteps
↑tilesVisited size
timesSteppedOn: aTile
↑tilesVisited occurrencesOf: aTile
private
setVariables
currentTile ← Tile new.
tilesVisited ← Bag new
|
We can now send the following messages in order to experiment with a drunken cockroach. Initialize the class and create an instance.
DrunkenCockroach initialize.
cockroach ← DrunkenCockroach new
Obtain the results of 10 experiments with a 5 by 5 room.
results ← OrderedCollection new: 10.
10 timesRepeat:
[cockroach walkWithin: (1 @ 1 cornet: 5 @ 5) startingAt: (1 @ 1).
results add: cockroach numberOfSteps]
The average of the 10 results is the average number of steps it took the drunken cockroach to solve the problem.
(results inject: 0 into: [ :sum :exp | sum + exp]) / 10
Note that in the implementation of the DrunkenCockroach message walkWithin:startingAt:, the termination condition is whether the Bag, when converted to a Set, has N*M elements. A faster way to make this test would be to add the message uniqueElements to the class Bag so that the conversion to a Set is not done each time through the iteration.
(For those readers wishing to try this change, the method to be added to class Bag is
uniqueElements
↑contents size
Then the message walkWithin:startingAt: can be changed so that the termination condition is tilesVisited uniqueElements < numberTiles.)
Traversing Binary Trees
A tree is an important nonlinear data structure that is useful in computer algorithms. A tree structure means that there is a branching relationship between elements. There is one element designated as the root of the tree. If there is only one element, then it is the root. If there are more elements, then they are partitioned into disjoint (sub)trees. A binary tree is either the root only, the root with one binary (sub)tree, or the root together with two binary (sub)trees. A complete description of the genealogy of tree structures is provided by Knuth in Volume 1 of the Art of Computer Programming. Here we assume the reader is familiar with the idea so that we can demonstrate how to specify the data structure as a Smalltalk-80 class.
We will define a class Tree in a way that corresponds to the definition of LinkedList. Elements of a Tree will be Nodes that are like the Links of LinkedLists, able to make connections to other elements. The Tree will reference the root node only.
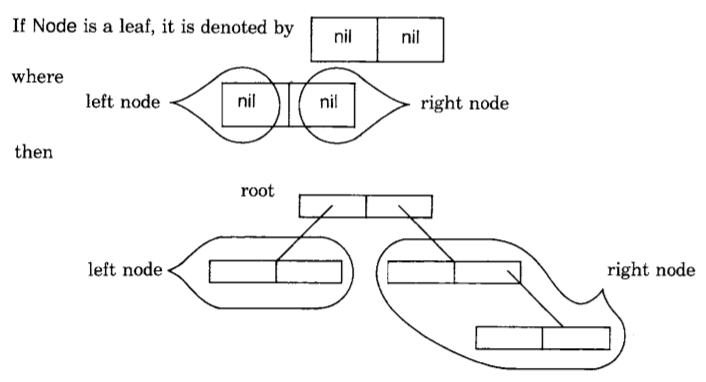
A node is simple to represent as a Smalltalk-80 object with two instance variables, one refers to the left node and another to the right node. We choose to treat the order of the nodes to support in-order traversal. That is, in enumerating the nodes, visit the left subnode first, the root second, and the right subnode third. If a node has no subnodes, then it is called a leaf We define the size of the node to be 1 plus the size of its subnodes, if any. Thus a leaf is a node of size 1, and a node with two leaves as subnodes has size 3. The size of a tree is the size of its root node. This definition of size corresponds to the general notion of size for collections.
Messages to a Node give access to the left node, the right node, and the last or end node. It is also possible to remove a subnode (remove:ifAbsent:) and the root (rest).
| class name | Node |
| superclass | Object |
| instance variable names | leftNode rightNode |
| class methods | instance creation
left: lNode right: rNode
"Create an instance of a Node with the arguments lNode and rNode as the left and right subnodes, respectively."
| newNode|
newNode ← self new.
newNode left: lNode.
newNode right: rNode.
↑newNode
|
| instance methods | testing
isLeaf
"Answer whether the receiver is a leaf, that is, whether it is a node without any subnodes."
↑leftNode isNil & rightNode isNil
accessing
left
↑leftNode
left: aNode
leftNode ← aNode
right
↑rightNode
right: aNode
rightNode ← aNode
size
↑1 + (leftNode isNil
ifTrue: [0]
ifFalse: [leftNode size])
+ (rightNode isNil
ifTrue: [0]
ifFalse: [rightNode size])
end
| aNode |
aNode ← self.
[aNode right isNil] whileFalse: [aNode ← aNode right].
↑aNode
removing
remove: subnode ifAbsent: exceptionBlock
"Assumes the root, self, is not the one to remove."
self isLeaf ifTrue: [↑exceptionBlock value].
leftNode = subnode
ifTrue: [leftNode ← leftNode rest. ↑subnode].
rightNode = subnode
ifTrue: [rightNode ← rightNode rest. ↑subnode].
leftNode isNil
ifTrue: [↑rightNode remove: subnode ifAbsent: exceptionBlock].
↑leftNode
remove: subnode
ifAbsent:
[rightNode isNil
ifTrue: [exceptionBlock value]
ifFalse:
[rightNode remove: subnode
ifAbsent: exceptionBlock]]
rest
leftNode isNil
ifTrue: [↑rightNode]
ifFalse: [leftNode end right: rightNode.
↑leftNode]
enumerating
do: aBlock
leftNode isNil ifFalse: [leftNode do: aBlock].
aBlock value: self.
rightNode isNil ifFalse: [rightNode do: aBlock]
|
Enumeration uses in-order traversal, first applying the left subnode as the value of the block, then the root, and third the right subnode. The block must be defined for a block argument that is a Node.
Next we provide a Tree as a kind of SequenceableCollection whose elements are Nodes. A Tree has one instance variable which we name root; root is either nil or it is an instance of Node. As a subclass of SequenceableCollection, class Tree implements messages add: anElement, remove: anElement ifAbsent: exceptionBlock, and do: aBlock. Basically, the methods associated with each of these messages checks to see whether the tree is empty (root isNil) and, if not, passes the appropriate message to root. The check on "empty" is inherited from Collection. The intention is that the programmer who uses a tree structure accesses the elements of that structure only via an instance of class Tree.
| class name | Tree |
| superclass | SequenceableCollection |
| instance variable names | root |
| instance methods | testing
isEmpty
↑root isNil
accessing
first
| save |
self emptyCheck.
save ← root.
[save left isNil] whileFalse: [save ← save left].
↑save
last
self emptyCheck.
↑root end
size
self isEmpty
ifTrue: [↑0]
ifFalse: [↑root size]
adding
add: aNode
↑self addLast: aNode
addFirst: aNode
"If the collection is empty, then the argument, aNode, is the new root; otherwise, it is the left node of the current first node."
self isEmpty
ifTure: [↑root ← aNode]
ifFalse: [self first left: aNode].
↑aNode
addLast: aNode
"If the collection is empty, then the argument, aNode, is the new root; otherwise it is the last element of the current root."
self isEmpty
ifTrue: [root ← aNode]
ifFalse: [self last right: aNode].
↑aNode
removing
remove: aNode ifAbsent: exceptionBlock
"First check the root. If not found, move down the tree checking each node."
self isEmpty ifTrue: [↑exceptionBlock value].
root = aNode
ifTrue: [root ← root rest. ↑aNode]
ifFalse: [↑root remove: aNode ifAbsent: exceptionBlock]
removeFirst
self emptyCheck.
↑self remove: self first ifAbsent: []
removeLast
self emptyCheck.
↑self remove: self last ifAbsent: []
enumerating
do: aBlock
self isEmpty ifFalse: [root do: aBlock]
|
Note that the removing messages do not remove the subtree beginning with the node to be removed, only the node itself.
A Binary Word Tree
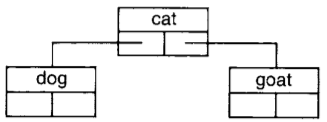
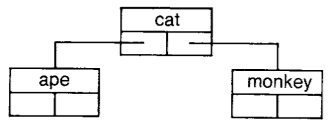
The definition of a Node, like that of a Link, is all structure without content. We have left the content of each Node to be specified by a subclass. Suppose we wish to use a kind of Node to store words represented as Strings. We call this class WordNode. An instance of WordNode is created by sending WordNode the message for:, if no subnodes are specified, or for:left:right: if the two subnodes are specified. So a WordNode illustrated as
is created by evaluating the expression
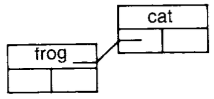
WordNode for: 'cat'
A WordNode that looks like
is created by evaluating the expression
WordNode for: 'cat'
left: (WordNode for: 'dog')
right: (WordNode for: 'goat')
An implementation for the class WordNode follows. Notice that equality (=) is redefined to mean that the words in the Nodes are the same; this means that the inherited removing messages will remove a subnode if its word is the same as the word of the argument.
| class name | WordNode |
| superclass | Node |
| instance variable names | word |
| class methods | instance creation
for: aString
↑self new word: aString
for: aString left: lNode right: rNode
| newNode |
newNode ← super left: lNode right: rNode.
newNode word: aString.
↑newNode
|
| instance methods | accessing
word
↑word
word: aString
word ← aString
comparing
= aWordNode
↑(aWordNode isKindOf: WordNode) and: [word = aWordNode word]
hash
↑word hash
|
A sequence of expressions follows to illustrate the use of WordNode. Note that no effort is made in the definition of WordNode to support inserting elements so that each word collates alphabetically when the tree is traversed. An interested reader might add an insert: aWordNode message to WordNode that maintains the alphabetic sort.
tree ← Tree new.
tree add: (WordNode for: 'cat')
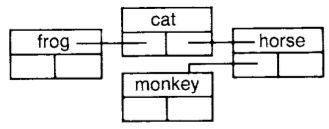
tree addFirst: (WordNode for: 'frog')
tree addLast: (WordNode for: 'horse' left: (WordNode for: 'monkey') right: nil)
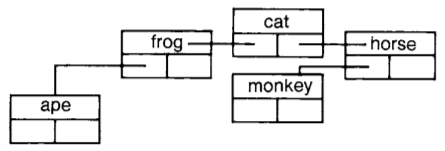
tree addFirst: (WordNode for: 'ape')
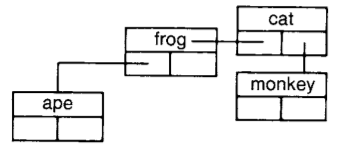
tree remove: (WordNode for: 'horse')
tree remove: (WordNode for: 'frog')