Smalltalk80LanguageImplementation:Chapter 10
- Chapter 10 Hierarchy of the Collection Classes
Hierarchy of the Collection Classes
Object
Magnitude
Character
Date
Time
Number
Float
Fraction
Integer
LargeNegativeInteger
LargePositiveInteger
SmallInteger
LookupKey***
Association***
Link***
Process
Collection
SequenceableCollection***
LinkedList***
Semaphore
ArrayedCollection***
Array***
Bitmap
DisplayBitmap
RunArray***
String***
Symbol***
Text***
ByteArray***
Interval***
OrderedCollection***
SortedCollection***
Bag***
MappedCollection***
Set***
Dictionary***
IdentifyDictionary***
Stream
PositionableStream
ReadStream
WriteStream
ReadWriteStream
ExternalStream
FileStream
Random
File
FileDirectory
FilePage
UndefinedObject
Boolean
False
True
ProcessorScheduler
Delay
SharedQueue
Behavior
ClassDescription
Class
MetaClass
Point
Rectangle
BitBit
CharacterScanner
Pen
DisplayObject
DisplayMedium
Form
Cursor
DisplayScreen
InfiniteForm
OpaqueForm
Path
Arc
Circle
Curve
Line
LinearFit
Spline
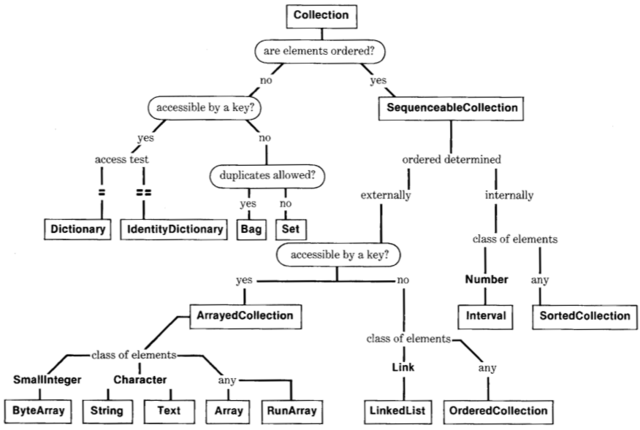
Figure 10.1 provides a road map for distinguishing among the various collection classes in the system. Following the choices in the figure is a useful way to determine which kind of collection to use in an implementation.
One distinction among the classes is whether or not a collection has a well-defined order associated with its elements. Another distinction is that elements of some collections can be accessed through externally-known names or keys. The type of key defines another way of distinguishing among kinds of collections. Some are integer indices, implicitly assigned according to the order of the elements; others are explicitly assigned objects that serve as lookup keys.
One unordered collection with external keys is a Dictionary. Its keys are typically instances of String or LookupKey; the comparison for matching keys is equality (=). Dictionary has a subclass, IdentityDictionary, whose external keys are typically Symbols. Its comparison for matching keys is equivalence (= =). Elements of a Bag or a Set are unordered and not accessible through externally-known keys. Duplicates are allowed in a Bag, but not allowed in a Set.
All ordered collections are kinds of SequenceableCollections. Elements of all SequenceableCollections are accessible through keys that are integer indices. Four subclasses of SequenceableCollection support different ways in which to create the ordering of elements. An additional distinction among the SequenceableCollection classes is whether the elements can be any object or whether they are restricted to be instances of a particular kind of object.
The order of elements is determined externally for OrderedCollections, LinkedLists, and ArrayedCollections. For OrderedCollection and LinkedList,the programmer's sequencefor adding and removing elements defines the ordering of the elements. An element of an OrderedCollection can be any object, while that of a LinkedList must be a kind of kink. The different ArrayedCollections in the system include Array, String, and ByteArray. The elements of an Array or a RunArray can be any kind of object, elements of a String or of a Text must be Characters, and those of a ByteArray must be SmallIntegers between 0 and 255.
The order of elements is determined internally for Intervals and SortedCollections. For an Interval, the ordering is an arithmetic progression that is specified at the time the instance is created. For a SortedCollection, the ordering is specified by a sorting criterion determined by evaluating a block known to the collection. Elements of an Interval must be Numbers; elements of a SortedCollection can be any kind of object.
In addition to the collection classes already mentioned, MappedCollection is a Collection that represents an indirect access path to a collection whose elements are accessible via external keys. The mapping from one set of external keys to the collection is determined at the time the MappedCollection is created.
The remainder of this chapter explores each of the collection subclasses, describing any additions to the message protocols and providing simple examples.
Class Bag
A Bag is the simplest kind of collection. It represents collections whose elements are unordered and have no external keys. It is a subclass of Collection. Since its instances do not have external keys, they cannot respond to the messages at: and at:put:. The message size answers the total number of elements in the collection.
A Bag is nothing more than a group of elements that behaves according to the protocol of all collections. The general description of collections does not restrict the number of occurrences of an element in an individual collection. Class Bag emphasizes this generality by specifying an additional message for adding elements.
| adding | |
| add: newObject withOccurrences: anInteger | Include the argument, newObject, as an element of the receiver, anInteger number of times. Answer the argument, newObject. |
| Bag instance protocol | |
Consider the example class Product which represents a grocery item and its price. A new Product may be created using the message of: name at: price, and the price of an instance is accessible by sending it the message price. Filling one's grocery bag may be expressed by
sack ← Bag new.
sack add: (Product of: #steak at: 5.80).
sack add: (Product of: #potatoes at: 0.50) with Occurrences: 6.
sack add: (Product of: #carrots at: 0.10) withOccurrences: 4.
sack add: (Product of: #milk at: 2.20)
Then the grocery bill is determined by the expression
amount ← 0.
sack do: [ :eachProduct | amount ← amount + eachProduct price]
or
sack inject: 0
into: [ :amount :eachProduct | amount + eachProduct price]
to be $11.40. Note that the messages add:, do:, and inject:into: to a Bag are inherited from its superclass, Collection.
A Bag is unordered, so that, although enumeration messages are supported, the programmer cannot depend on the order in which elements are enumerated.
Class Set
Class Set represents collections whose elements are unordered and have no external keys. Its instances cannot respond to the messages at: and at:put:. A Set is like a Bag except that its elements cannot be duplicated. The adding messages add the element only if it is not already in the collection. Class Set is a subclass of class Collection.
Classes Dictionary and IdentityDictionary
Class Dictionary represents a set of associations between keys and values. The elements of a Dictionary are instances of class Association, a simple data structure for storing and retrieving the members of the key-value pair.
An alternative way of thinking about a Dictionary is that it is a collection whose elements are unordered but have explicitly assigned keys or names. From this perspective, the elements of a Dictionary are arbitrary objects (values) with external keys. These alternative ways of thinking about a Dictionary are reflected in the message protocol of the class. Messages inherited from class Collection--includes:, do:, and other enumeration messages--are applied to the values of the Dictionary. That is, these messages refer to the values of each association in the Dictionary, rather than to the keys or to the associations themselves.
Messages inherited from class Object--at: and at:put:mare applied to the keys of the Dictionary. The at: and at:put: paradigm is extended for the associations and the values by adding messages associationAt: and keyAtValue:. In order to provide additional control when looking up elements in a Dictionary, the message at:ifAbsent: is provided; using it, the programmer can specify the action to take if the element whose key is the first argument is not found. The inherited message at: reports an error if the key is not found.
| accessing | |
| at: key ifAbsent: aBlock | Answer the value named by the argument, key. If key is not found, answer the result of evaluating aBlock. |
| associationAt: key | Answer the association named by the argument, key. If key is not found, report an error. |
| associationAt: key ifAbsent: aBlock | Answer the association named by the argument, key. If key is not found, answer the result of evaluating aBlock. |
| keyAtValue: value | Answer the name for the argument, value. If there is no such value, answer nil. Since values are not necessarily unique, answer the name for the first one encountered in the search. |
| keyAtValue: value ifAbsent: exceptionBlock | Answer the key for the argument, value. If there is no such value, answer the result of evaluating exceptionBlock. |
| keys | Answer a Set containing the receiver's keys. |
| values | Answer a Bag containing the receiver's values (includes any duplications). |
| Dictionary instance protocol | |
As an example of the use of a Dictionary, suppose opposites is a Dictionary of word Symbols and their opposites.
opposites ← Dictionary new.
opposites at: #hot put: #cold.
opposites at: #push put: #pull.
opposites at: #stop put: #go.
opposites at: #come put: #go
Alternatively, an element can be added using the message add: by creating an Association as the argument.
opposites add: (Association key: #front value: #back).
opposites add: (Association key: #top value: #bottom)
The Dictionary, opposites, now consists of
| key | value |
| hot | cold |
| push | pull |
| stop | go |
| come | go |
| front | back |
| top | bottom |
We can use the testing protocol inherited from class Collection to test the values in the Dictionary. Notice that includes: tests the inclusion of a value, not a key.
| expression | result |
| opposites size | 6 |
| opposites includes: #cold | true |
| opposites includes: #hot | false |
| opposites occurrencesOf: #go | 2 |
| opposites at: #stop put: #start | start |
The fourth example indicates that, although a key can appear only once in a Dictionary, a value can be associated with any number of keys. The last example re-associates the key #stop with a new value, #start. Additional messages are provided in class Dictionary for testing associations and keys.
| dictionary testing | |
| includesAssociation: anAssociation | Answer whether the receiver has an element (association between a key and a value) that is equal to the argument, anAssociation. |
| includesKey: key | Answer whether the receiver has a key equal to the argument, key. |
| Dictionary instance protocol | |
Then we can try
| expression | result |
| opposites includesAssociation:(Association key: #come value: #go) | true |
| opposites includesKey: #hot | true |
Similarly, the removing protocol specified in class Collection is extended to provide access by reference to associations and keys, as well as to values. However, the message remove: itself is not appropriate for a Dictionary; in removing an element, mention of the key is required.
| dictionary removing | |
| removeAssociation: anAssociation | Remove the key and value association, anAssociation, from the receiver. Answer anAssociation. |
| removeKey: key | Remove key (and its associated value) from the receiver. If key is not in the receiver, report an error. Otherwise, answer the value associated with key. |
| removeKey: key ifAbsent: aBlock | Remove key (and its associated value) from the receiver. If key is not in the receiver, answer the result of evaluating aBlock. Otherwise, answer the value named by key. |
| Dictionary instance protocol | |
For example
| expression | result |
| opposites removeAssociation: (Association key: #top value: #bottom) | The association whose key is #top and value is #bottom. opposites has one less element. |
| opposites removeKey: #hot | The association whose key is #hot and whose value is #cold. This association is removed from opposites. |
| opposites removeKey: #cold ifAbsent: [opposites at: #cold put: #hot] | hot |
As a result of the last example, the association of #cold with :#:hot is now an element of opposites.
The message do: evaluates its argument, a block, for each of the Dictionary's values. The collection enumerating protocol, inherited from class Collection, is again extended in order to provide messages for enumerating over the associations and the keys. Messages supporting uses of reject: and inject:into: are not provided.
| dictionary enumerating | |
| associationsDo: aBlock | Evaluate aBlock for each of the receiver's key/value associations. |
| keysDo: aBlock | Evaluate aBlock for each of the receiver's keys. |
| Dictionary instance protocol | |
We thus have three possible ways of enumerating over a Dictionary. Suppose newWords is a Set of vocabulary words that a child has not yet learned. Any word in opposites is now part of the child's repertoire and can be removed from newWords. Evaluating the following two expressions removes these words (the first removes the values, the second the keys).
opposites do: [ :word | newWords remove: word ifAbsent: []].
opposites keysDo: [ :word | newWords remove: word ifAbsent: []]
Note that if a word from opposites is not in newWords, then nothing (no error report) happens. Alternatively, one expression, enumerating the Associations, can be used.
opposites associationsDo:
[ :each |
newWords remove: each key ifAbsent: [].
newWords remove: each value ifAbsent: []]
The accessing messages keys and values can be used to obtain collections of the words in the opposites dictionary. Assuming the evaluation of all previous example expressions, then
opposites keys
returns the Set whose elements are
push come front stop cold
and
opposites values
returns the Bag whose elements are
pull go back start hot
Class SequenceableCollection
Class SequenceableCollection represents collections whose elements are ordered and are externally named by integer indices. SequenceableCollection is a subclass of Collection and provides the protocol for accessing, copying, and enumerating elements of a collection when it is known that there is an ordering associated with the elements. Since the elements are ordered, there is a well-defined first and last element of the collection. It is possible to ask the index of a particular element (indexOf:) and the index of the beginning of a sequence of elements within the collection (indexOfSubCollection:startingAt:). All collections inherit messages from class Object for accessing indexed variables. As described in Chapter 6, these are at:, at:put:, and size. In addition, SequenceableCollections support putting an object at all positions named by the elements of a Collection (atAll:put:), and putting an object at all positions in the sequence (atAllPut:). Sequences of elements within the collection can be replaced by the elements of another collection (replaceFrom:to:with: and replaceFrom:to:with:startingAt:).
| accessing | |
| atAll: aCollection put: anObject | Associate each element of the argument, aCollection (an Integer or other external key), with the second argument, anObject. |
| atAllPut: anObject | Put the argument, anObject, as every one of the receiver's elements. |
| first | AAnswer the first element of the receiver. Report an error if the receiver contains no elements. |
| last | Answer the last element of the receiver. Report an error if the receiver contains no elements. |
| indexOf: anElement | AAnswer the first index of the argument, anElement, within the receiver. If the receiver does not contain anElement, answer 0. |
| indexOf: anElement ifAbsent: exception Block | Answer the first index of the argument, anElement, within the receiver. If the receiver does not contain anElement, answer the result of evaluating the argument, exceptionBlock. |
| indexOfSubCollection: aSubCollection startingAt: anIndex | If the elements of the argument, aSubCollection, appear, in order, in the receiver, then answer the index of the first element of the first such occurrence. If no such match is found, answer 0. |
| indexOfSubCollection: aSubCollection startingAt: anIndex ifAbsetnt: exceptionBlock | Answer the index of the receiver's first element, such that that element equals the first element of the argument, aSubCollection, and the next elements equal the rest of the elements of aSubCollection. Begin the search of the receiver at the element whose index is the argument, anIndex. If no such match is found, answer the result of evaluating the argument, exceptionBlock. |
| replaceFrom: start to: stop with: replacementCollection | Associate each index between start and stop with the elements of the argument, replacementCollection. Answer the receiver. The number of elements in replacementCollection must equal stop-start + 1. |
| replaceFrom: start to: stop with: replacementCollection startingAt: repStart | Associate each index between start and stop with the elements of the argument, replacementCollection, starting at the element of replacementCollection whose index is repStart. Answer the receiver. No range checks are performed, except if the receiver is the same as replacementCollection but repStart is not 1, then an error reporting that indices are out of range will occur. |
| SequenceableCollection instance protocol | |
Examples of using these accessing messages, using instances of String, are
| expression | result |
| 'aaaaaaaaaa' size | 10 |
| 'aaaaaaaaaa' atAll: (2 to: 10 by: 2) put: $b | 'ababababab' |
| 'aaaaaaaaaa' atAllPut: $b | 'bbbbbbbbbb' |
| 'This string' first | $T |
| 'This string' last | $g |
| 'ABCDEFGHIJKLMNOP' indexOf: $F | 6 |
| 'ABCDEFGHIJKLMNOP' indexof: $M ifAbsent: [0] | 13 |
| 'ABCDEFGHIJKLMNOP' indexOf: $Z ifAbsent: [0] | 0 |
| 'The cow jumped' indexOfSubCollection: 'cow' startingAt: 1 | 5 |
| 'The cow jumped' replaceFrom: 5 to: 7 with: 'dog' | 'The dog jumped' |
| 'The cow jumped' replaceFrom: 5 to: 7 with: 'the spoon ran' startingAt: 5 | 'The spo jumped' |
Any of these examples could be similarly carried out with an instance of any subclass of SequenceableCollection, for example, with an Array. For the Array, @(The brown jug), replacement of brown by black is carried out by evaluating the expression
#(The brown jug) replaceFrom: 2 to: 2 with: #(black)
Notice that the last argument must be an Array as well. And notice that the replacement messages do not change the size of the original collection (the receiver), although they do alter the collection. It may be preferrable to preserve the original by creating a copy. The copying protocol of SequenceableCollections supports copying a sequence of elements in the collection, copying the entire collection with part of it replaced, copying the entire collection with an element deleted, or copying the entire collection with one or more elements concatenated.
| copying | |
| , aSequenceableCollection | This is the concatenation operation. Answer a copy of the receiver with each element of the argument, aSequenceableCollection, added, in order. |
| copyFrom: start to: stop | Answer a copy of a subset of the receiver, starting from element at index start until element at index stop. |
| copyReplaceAll: oldSubCollection with: newSubCollection | Answer a copy of the receiver in which all occurrences of oldSubCollection have been replaced by newSubCollection. |
| copyReplaceFrom: start to: stop with: replacementCollection | Answer a copy of the receiver satisfying the following conditions: If stop is less than start, then this is an insertion; stop should be exactly start-1, start = 1 means insert before the first character, start = size + 1 means append after last character. Otherwise, this is a replacement; start and stop have to be within the receiver's bounds. |
| copyWith: newElement | Answer a copy of the receiver that is 1 bigger than the receiver and has newElement as the last element. |
| copyWithout: oldElement | Answer a copy of the receiver in which all occurrences of oldElement have been left out. |
| SequenceableCollection instance protocol | |
Using the replace and copy messages, a simple text editor can be devised. The Smalltalk-80 system includes class String as well as-class Text, the latter providing support for associating the characters in the String with font or emphasis changes in order to mix character fonts, bold, italic, and underline. The message protocol for Text is that of a SequenceableCollection with additional protocol for setting the emphasis codes. For illustration purposes, we use an instance of class String, but remind the reader of the analogous application of editing messages for an instance of class Text. Assume that line is initially an empty string
line ← String new: 0
Then
| expression | result |
| line ← line copyReplaceFrom: 1 to: 0 with: 'this is the first line tril' | 'this is the first line tril' |
| line ← line copyReplaceAll: 'tril' with: 'trial' | 'this is the first line trial' |
| line ← line copyReplaceFrom: (line size + 1) to: (line size) with: 'and so on' | this is the first line trial and so on' |
| line indexOfSubCollection: 'trial' startingAt: 1 | 24 |
| line ← line copyReplaceFrom: 29 to: 28 with: ' ' | 'this is the first line trial and so on' |
The last two messages of the copying protocol given above are useful in obtaining copies of an Array with or without an element. For example
| expression | result |
| #(one two three) copyWith: #four | (one two three four) |
| #(one two three) copyWithout: #two | (one three) |
Because the elements of a SequenceableCollection are ordered, enumeration is in order, starting with the first element and taking each successive element until the last. Reverse enumeration is also possible, using the message reverseDo: aBlock. Enumeration of two SequenceableCollections can be done together so that pairs of elements, one from each collection, can be used in evaluating a block.
| enumerating | |
| findFirst: aBlock | Evaluate aBlock with each of the receiver's elements as the argument. Answer the index of the first element for which the argument, aBlock evaluates to true. |
| findLast: aBlock | Evaluate aBlock with each of the receiver's elements as the argument. Answer the index of the last element for which the argument, aBlock evaluates to true. |
| reverseDo: aBlock | Evaluate aBlock with each of the receiver's elements as the argument, starting with the last element and taking each in sequence up to the first. For SequenceableCollections, this is the reverse of the enumeration for do:. aBlock is a one-argument block. |
| with: aSequenceableCollection do: aBlock | Evaluate aBlock with each of the receiver's elements along with the corresponding element from aSequenceableCollection. aSequenceableCollection must be the same size as the receiver, and aBlock must be a two-argument block. |
| SequenceableCollection instance protocol | |
The following expressions create the Dictionary, opposites, which was introduced in an earlier example.
opposites ← Dictionary new.
#(come cold front hot push stop)
with: #(go hot back cold pull start)
do: [ :key :value | opposites at: key put: value]
The Dictionary now has six associations as its elements.
Any SequenceableCollection can be converted to an Array or a MappedCollection. The messages are asArray and mappedBy: aSequenceableCollection.
SubClasses of SequenceableCollection
Subclasses of SequenceableCollection are OrderedCollection, LinkedList, Interval, and MappedCollection. ArrayedCollection is a subclass representing a collection of elements with a fixed range of integers as external keys. Subclasses of ArrayedCollection are, for example, Array and String.
Class OrderedCollection
OrderedCollections are ordered by the sequence in which objects are added and removed from them. The elements are accessible by external keys that are indices. The accessing, adding, and removing protocols are augmented to refer to the first and last elements, and to elements preceding or succeeding other elements.
OrderedCollections can act as stacks or queues. A stack is a sequential list for which all additions and deletions are made at one end of the list (called either the "rear" or the "front") of the list. It is often called a last-in first-out queue.
| usual vocabulary | OrderedCollection message |
| push newObject | addLast: newObject |
| pop | removeLast |
| top | last |
| empty | isEmpty |
A queue is a sequential list for which all additions are made at one end of the list (the "rear"), but all deletions are made from the other end (the "front"). It is often called a first-in first-out queue.
| usual vocabulary | OrderedCollection message |
| add newObject | addLast: newObject |
| delete | removeFirst |
| front | first |
| empty | isEmpty |
The message add: to an OrderedCollection means "add the element as the last member of the collection" and remove: means "remove the argument as an element." The message protocol for OrderedCollections, in addition to that inherited from classes Collection and SequenceableCollection, follows.
| accessing | |
| after: oldObject | Answer the element after oldObject in the receiver. If the receiver does not contain oldObject or if the receiver contains no elements after oldObject, report an error. |
| before: oldObject | Answer the element before oldObject in the receiver. If the receiver does not contain oldObject or if the receiver contains no elements before oldObject, report an error. |
| adding | |
| add: newObject after: oldObject | Add the argument, newObject, as an element of the receiver. Put it in the sequence just succeeding oldObject. Answer newObject. If oldObject is not found, then report an error. |
| add: newObject before: oldObject | Add the argument, newObject, as an element of the receiver. Put it in the sequence just preceding oldObject. Answer newObject. If oldObject is not found, then report an error. |
| addAllFirst: anOrderedCollection | Add each element of the argument, anOrderedCollection, at the beginning of the receiver. Answer anOrderedCollection. |
| addAllLast: anOrderedCollection | Add each element of the argument, anOrderedCollection, to the end of the receiver. Answer anOrderedCollection. |
| addFirst: newObject | Add the argument, newObject, to the beginning of the receiver. Answer newObject. |
| addLast: newObject | Add the argument, newObject, to the end of the receiver. Answer newObject. |
| removing | |
| removeFirst | Remove the first element of the receiver and answer it. If the receiver is empty, report an error. |
| removeLast | Remove the last element of the receiver and answer it. If the receiver is empty, report an error. |
| OrderedCollection instance protocol | |
Class SortedCollection
Class SortedCollection is a subclass of OrderedCollection. The elements in a SortedCollection are ordered by a function of two elements. The function is represented by a two-argument block called the sort block. It is possible to add an element only with the message add:; messages such as addLast: that allow the programmer to specify the order of inserting are disallowed for SortedCollections.
An instance of class SortedCollection can be created by sending SortedCollection the message sortBlock:. The argument to this message is a block with two-arguments, for example,
SortedCollection sortBlock: [ :a :b | a < = b ]
This particular block is the default sorting function when an instance is created simply by sending SortedCollection the message new. Thus examples of the four ways to create a SortedCollection are
SortedCollection new
SortedCollection sortBlock: [ :a :b | a > b ]
anyCollection asSortedCollection
anyCollection asSortedCollection: [ :a :b | a > b ]
It is possible to determine the block and to reset the block using two additional accessing messages to instances of SortedCollection. When the block is changed, the elements of the collection are, of course, re-sorted. Notice that the same message is sent to the class itself (sortBlock:) to create an instance with a particular sorting criterion, and to an instance to change its sorting criterion.
| instance creation | |
| sortBlock: aBlock | Answer an instance of SortedCollection such that its elements will be sorted according to the criterion specified in the argument, aBlock. |
| SortedCollection instance protocol | |
| accessing | |
| sortBlock | Answer the block that is the criterion for sorting elements of the receiver. |
| sortBlock: aBlock | Make the argument, aBlock, be the criterion for ordering elements of the receiver. |
| SortedCollection class protocol | |
Suppose we with to maintain an alphabetical list of the names of children in a classroom.
children ← s=SortedCollection new
The initial sorting criterion is the default block [ :a :b | a < = b]. The elements of the collection can be Strings or Symbols because, as we shall show presently, these kinds of objects respond to the comparison messages <, >, < =, and > =.
| expression | result |
| children add: #Joe | Joe |
| children add: #Bill | Bill |
| children add: #Alice | Alice |
| children | SortedCollection(Alice Bill Joe) |
| children add: #Sam | Sam |
| a < b ] | SortedCollection(Sam Joe Bill Alice) |
| children add: #Henrietta | Henrietta |
| children | SortedCollection(Sam Joe Henrietta Bill Alice) |
The sixth message in the example reversed the order in which elements are stored in the collection, children.
Class LinkedList
LinkedList is another subclass of SequenceableCollection whose elements are explicitly ordered by the sequence in which objects are added and removed from them. Like OrderedCollection, the elements of a LinkedList can be referred to by external keys that are indices. Unlike OrderedCollection, where the elements may be any object, the elements of a LinkedList are homogeneous; each must be an instance of class Link or of a subclass of Link.
A Link is a record of a reference to another Link. Its message protocol consists of three messages. The same message (nextLink:) is used to create an instance of Link with a particular reference, and to change the reference of an instance.
| instance creation | |
| nextLink: aLink | Create an instance of Link that references the argument, aLink. |
| LinkedList class protocol | |
| accessing | |
| nextLink | Answer the receiver's reference. |
| nextLink: aLink | Set the receiver's reference to be the argument, aLink. |
| LinkedList instance protocol | |
Since class Link does not provide a way to record a reference to the actual element of the collection, it is treated as an abstract class. That is, instances of it are not created. Rather, subclasses are defined that provide the mechanisms for storing one or more elements, and instances of the subclasses are created.
Since LinkedList is a subclass of SequenceableCollection, its instances can respond to the accessing, adding, removing, and enumerating messages defined for all collections. Additional protocol for LinkedList consists of
| adding | |
| addFirst: aLink | Add aLink to the beginning of the receiver's list. Answer aLink. |
| addLast: aLink | Add aLink to the end of the receiver's list. Answer aLink. |
| removing | |
| removeFirst | Remove the receiver's first element and answer it. If the receiver is empty, report an error. |
| removeLast | Remove the receiver's last element and answer it. If the receiver is empty, report an error. |
| LinkedList instance protocol | |
An example of a subclass of Link in the Smalltalk-80 system is class Process. Class Semaphore is a subclass of LinkedList. These two classes are discussed in Chapter 15, which is about multiple independent processes in the system.
The following is an example of the use of LinkedList. Link does not provide instance information other than a reference to another Link. So, as an example, assume that there is a subclass of Link named Entry. Entry adds the ability to store one object. The instance creation message for an Entry is for: anObject, and its accessing message is element.
| class name | Entry |
| superclass | Link |
| instance variable names | element |
| class methods | instance creation
for: anObject
↑self new setElement: anObject
|
| instance methods | accessing
element
↑element
printing
printOn: aStream
aStream nextPutAll: 'Entry for:', element printString
private
setElement: anObject
element ← anObject
|
The classes LinkedList and Entry can then be used as follows.
| expression | result |
| link ← LinkedList new | LinkedList () |
| list add: (Entry for: 2) | Entry for: 2 |
| list add: (Entry for: 4) | Entry for: 4 |
| list addLast: (Entry for: 5) | Entry for: 5 |
| list addFirst: (Entry for: 1) | Entry for: 1 |
| list | LinkedList (Entry for: 1 Entry for: 2 Entry for: 4 Entry for: 5) |
| list isEmpty | false |
| list size | 4 |
| (each element) + value ] | 12 |
| list last | Entry for: 5 |
| list first | Entry for: 1 |
| list remove: (Entry for:4) | Entry for: 4 |
| list removeFirst | Entry for: 1 |
| list removeLast | Entry for: 5 |
| list first = = list last | true |
Class Interval
Another kind of SequenceableCollection is a collection of numbers representing a mathematical progression. For example, the collection might consist of all the integers in the interval from 1 to 100; or it might consist of all even integers in the interval from 1 to 100. Or the collection might consist of a series of numbers where each additional number in the series is computed from the previous one by multiplying it by 2. The series might start with 1 and end with the last number that is less than or equal to 100. This would be the sequence 1, 2, 4, 8, 16, 32, 64.
A mathematical progression is characterized by a first number, a limit (maximum or minimum) for the last computed number, and a method for computing each succeeding number. The limit could be positive or negative infinity. An arithmetic progression is one in which the computation method is simply the addition of an increment. For example, it could be a series of numbers where each additional number in the series is computed from the previous one by adding a negative 20. The series might start with 100 and end with the last number that is greater than or equal to 1. This would be the sequence 100, 80, 60, 40, 20.
In the Smalltalk-80 system, the class of collections called Intervals consists of finite arithmetic progressions. In addition to those messages inherited from its superclasses SequenceableCollection and Collection, class Interval supports messages for initialization and for accessing those values that characterize the instance. New elements cannot be added or removed from an Interval.
The class protocol of Interval consists of the following messages for creating instances.
| instance creation | |
| from: startInteger to: stopInteger | Answer an instance of class Interval, starting with the number startInteger, ending with the number stopInteger, and using the increment 1 to compute each successive element. |
| from: startInteger to: stopInteger by: stepInteger | Answer an instance of Interval, starting with the number startInteger, ending with the number stopInteger, and using the increment stepInteger to compute each successive element. |
| Interval class protocol | |
All messages appropriate to SequenceableCollections can be sent to an Interval. In addition, the instance protocol of Interval provides a message for accessing the increment of the arithmetic progression (increment).
Class Number supports two messages that provide a shorthand for expressing new Intervals--to: stop and to" stop by: step. Thus to create an Interval of all integers from 1 to 10, evaluate either
Interval from: 1 to: 10
or
1 to: 10
To create an Interval starting with 100 and ending with 1, adding a negative 20 each time, evaluate either
Interval from: 100 to: 1 by: -20
or
100 to: 1 by: -20
This is the sequence 100, 80, 60, 40, 20. The Interval need not consist of Integers--to create an Interval between 10 and 40, incrementing by 0.2, evaluate either
Interval from: 10 to: 40 by: 0.2
or
10 to: 40 by: 0.2
This is the sequence 10, 10.2, 10.4, 10.6, 10.8, 11.0.... and so on.
Note that we could provide the more general case of a progression by replacing the numeric value of step by a block. When a new element is to be computed, it would be done by sending the current value as the argument of the message value: to the block. The computations of size and do: would have to take this method of computation into account.
The message do: to an Interval provides the function of the usual for-loop in a programming language. The Algol statement
for i := 10 step 6 until 100 do
begin
<statements>
end
is represented by
(10 to: 100 by: 6) do: [ :i | statements ]
Numbers respond to the message to:by:do: as though the expression had been written as given in the example. So that iteration can be written without parentheses as
10 to: 100 by: 6 do: [ :i | statements ]
To increment by 1 every sixth numeric element of an OrderedCollection, numbers, evaluate
6 to: numbers size
by: 6
do: [ :index | numbers at: index put: (numbers at: index) + 1 ]
The Interval created is 6, 12, 18.... , up to the index of the last element of numbers. If the size of the collection is less than 6 (the supposedly first index), nothing happens. Otherwise elements at position 6, 12, 18, and so on, until the last possible position, are replaced.
Class ArrayedCollection
As stated earlier, class ArrayedCollection is a subclass of Collection. It represents a collection of elements with a fixed range of integers as external keys. ArrayedCollection has five subclasses in the Smalltalk-80 system--Array, String, Text, RunArray, and ByteArray.
An Array is a collection whose elements are any objects. It provides the concrete representation for storing a collection of elements that have integers as external keys. Several examples of the use of Arrays have already been given in this chapter.
A String is a collection whose elements are Characters. Many examples of the use of Strings have been given in this and in previous chapters. Class String provides additional protocol for initializing and comparing its instances.
Text represents a String that has font and emphasis changes. It is used in storing information needed for creating textual documents in the Smalltalk-80 system. An instance of Text has two instance variables, the String and an instance of RunArray in which an encoding of the font and emphasis changes is stored.
Class RunArray provides a space-efficient storage of data that tends to be constant over long runs of the possible indices. It stores repeated elements singly and then associates with each single element a number that denotes the consecutive occurrences of the element. For example, suppose the Text representing the String 'He is a good boy.' is to be displayed with the word "boy" in bold, and further suppose that the code for the font is 1 and for its boldface version is 2. Then the RunArray for the Text that is associated with "He is a good boy." (a String of 17 Characters) consists of 1 associated with 13, 2 associated with 3, and 1 associated with 1. That is, the first 13 Characters are in font 1, the next three in font 2, and the last in font 1.
A ByteArray represents an ArrayedCollection whose elements are integers between 0 and 255. The implementation of a ByteArray stores two bytes to a 16-bit word; the class supports additional protocol for word and double-word access. ByteArrays are used in the Smalltalk-80 system for storing time in milliseconds.
Class String
As stated earlier, the class protocol for String adds messages for creating a copy of another String (fromString: aString) or for creating a String from the Characters in a Stream (readFrom: aStream). The main significance of this second message is that pairs of embedded quotes are read and stored as one element, the quote character. In addition, class String adds comparing protocol like that specified in class Magnitude. We introduced some of these messages earlier in the description of class SortedCollection.
| comparing | |
| < aString | Answer whether the receiver collates before the argument, aString. The collation sequence is ASCII with case differences ignored. |
| < = aString | Answer whether the receiver collates before the argument, aString, or is the same as aString. The collation sequence is ASCII with case differences ignored. |
| > aString | Answer whether the receiver collates after the argument, aString. The collation sequence is ASCII with case differences ignored. |
| > = aString | Answer whether the receiver collates after the argument, aString, or is the same as aString. The collation sequence is ASCII with case differences ignored. |
| match: aString | Treat the receiver as a pattern that can contain characters # and *. Answer whether the argument, aString, matches the pattern in the receiver. Matching ignores upper/lower case differences. Where the receiver contains the character #, aString may contain any single character. Where the receiver contains *, aString may contain any sequence of characters, including no characters. |
| sameAs: aString | Answer whether the receiver collates precisely with the argument, aString. The collation sequence is ASCII with case differences ignored. |
| String instance protocol | |
We have not as yet given examples of using the last two messages.
| expression | result |
| 'first string' sameAs: 'first string' | true |
| 'First String' sameAs: 'first string' | true |
| 'First String' = 'first string' | false |
| '#irst string' match: 'first string' | true |
| '*string' match: 'any string' | true |
| '*.st' match: 'filename.st' | true |
| 'first string' match: 'first *' | false |
Strings can be converted to all lowercase characters or all uppercase characters. They can also be converted to instances of class Symbol.
| converting | |
| asLowercase | Answer a String made up from the receiver whose characters are all lowercase. |
| asUppercase | Answer a String made up from the receiver whose characters are all uppercase. |
| asSymbol | Answer the unique Symbol whose characters are the characters of the receiver. |
| String instance protocol | |
Therefore we have
| expression | result |
| 'first string' asUppercase | 'FIRST STRING' |
| 'First String' asLowercase | 'first string' |
| 'First' asSymbol | First |
Class Symbol
Symbols are arrays of Characters that are guaranteed to be unique. Thus
'a string' asSymbol = = 'a string' asSymbol
answers true. Class Symbol provides two instance creation messages in its class protocol for this purpose.
| instance creation | |
| intern: aString | Answer a unique Symbol whose characters are those of aString. |
| internCharacter: aCharacter | Answer a unique Symbol of one character, the argument, aCharacter. |
| Symbol class protocol | |
In addition, Symbols can be expressed literally using the character # as a prefix to a sequence of Characters. For example, #dave is a Symbol of four Characters. Symbols print without this prefix notation.
Class MappedCollection
Class MappedCollection is a subclass of Collection. It represents an access mechanism for referencing a subcollection of a collection whose elements are named. This mapping can determine a reordering or filtering of the elements of the collection. The basic idea is that a MappedCollection refers to a domain and a map. The domain is a Collection that is to be accessed indirectly through the external keys stored in the map. The map is a Collection that associates a set of external keys with another set of external keys. This second set of keys must be external keys that can be used to access the elements of the domain. The domain and the map, therefore, must be instances of Dictionary or of a Subclass of SequenceableCollection.
Take, for example, the Dictionary of word Symbols, opposites, introduced earlier.
| key | value |
| come | go |
| cold | hot |
| front | back |
| hot | cold |
| push | pull |
| stop | start |
Suppose we create another Dictionary of synonym Symbols for some of the keys of the entries in opposites and refer to it by the variable name alternates.
| key | value |
| cease | stop |
| enter | come |
| scalding | hot |
| shove | push |
Then we can provide a MappedCollection by evaluating the expression
words ← MappedCollection collection: opposites map: alternates
Through words, we can access the elements of opposites. For example, the value of the expression words at: #cease is start (i.e., the value of the key cease in alternatives is stop; the value of the key stop in opposites is start). We can determine which part of opposites is referenced by words by sending words the message contents.
words contents
The result is a Bag containing the symbols start go cold pull.
The message at:put: is an indirect way to change the domain collection. For example
| expression | result |
| words at: #scalding | cold |
| words at: #cease | start |
| words at: #cease put: #continue | continue |
| opposites at: #stop | continue |
Summary of Conversions Among Collections
In the sections describing the various kinds of collections, we have indicated which collections can be converted to which other collections. In summary, any collection can be converted to a Bag, a Set, an OrderedCollection, or a SortedCollection. All collections except Bags and Sets can be converted to an Array or a MappedCollection. Strings and Symbols can be converted into one another; but no collection can be converted into an Interval or a LinkedList.