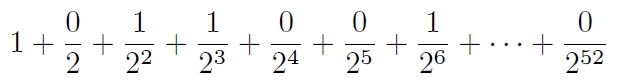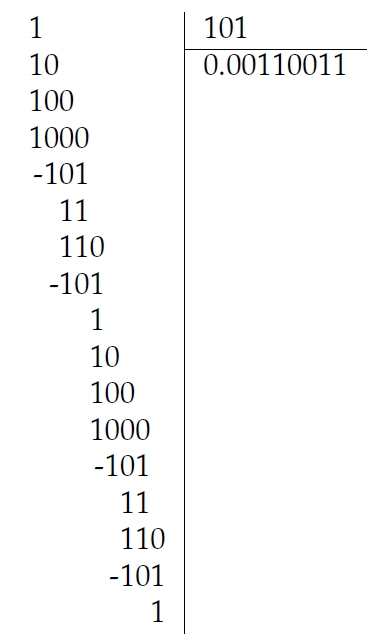DeepintoPharo:Chapter 16

제 16 장 Floats 갖고 놀기

Floats 갖고 놀기

Nicolas Cellier 참여 (nicolas.cellier.aka.nice@gmail.com)

Floats는 그 특성상 정밀하지 않아 프로그래머들을 헷갈리게 만들기도 한다. 따라서 본 장에서는 이러한 문제를 소개하고 실용적인 해결책을 몇 가지 제시하고자 한다. Floats는 다른 것이 아니라 부정확하지만 빠른 숫자라는 것이 기본 메시지다.

본 장에 설명된 대부분의 상황은 Floats가 하드웨어에 의해 구성되고 Pharo에 관련되지 않은 결과다. 다른 프로그래밍 언어에서도 마찬가지로 발생할 수 있는 문제다.

floats를 대상으로 동등성(equality)을 절대 테스트하지 말라

첫 번째 기본 규칙은 float 동등성을 절대로 비교하지 않는 것이다. 간단한 예를 들어보자. 두 개의 float를 더해도 그들의 합을 표현하는 float와 같지 않다. 예를 들어, 0.1+0.2는 0.3이 아니란 뜻이다.

(0.1 + 0.2) = 0.3
    → false

예상치 못했을 것이다. 학교에서 배운 내용이 아니다, 안 그런가? 이는 사실 놀라운 행위지만 floats는 부정확한 숫자이므로 정상이다. 이해해야 할 중요한 사항이 있다면, floats이 출력되는 방식 또한 우리의 이해에 영향을 미친다는 사실이다. 일부 접근법들은 다른 접근법들에 비해 사실을 더 간단히 표현하여 출력한다. 0.1+0.2를 출력하면, Pharo의 초기 버전들은 0.3을 출력했지만 지금은 0.30000000000000004를 출력한다. 이러한 변화는 사용자에게 거짓말을 하지 않는 편이 더 낫다는 개념에서 비롯된다. float의 부정확성이 오히려 숨기는 것보다 나은데, 언젠가 큰 코를 다치게 될 일이 발생할지도 모르기 때문이다.

(0.2 + 0.1) printString
    → '0.30000000000000004'
0.3 printString
    → '0.3'

16진 값을 살펴보면 두 개의 숫자를 확인할 수 있다.

(0.1 + 0.2) hex
    → '3FD3333333333334'
0.3 hex
    → '3FD3333333333333'

storeString 메서드 또한 두 개의 숫자가 있음을 전달한다.

(0.1 + 0.2) storeString
    → '0.30000000000000004'
0.3 storeString
    → '0.3'

closeTo:에 관하여. 두 개의 floats가 거의 같은 숫자처럼 보일 만큼 충분히 가깝다는 사실을 알기 위해선 closeTo: 메시지를 사용한다.

(0.1 + 0.2) closeTo: 0.3
    → true
0.3 closeTo: (0.1 + 0.2)
    → true

closeTo: 메서드는 비교 대상인 두 숫자의 차이가 0.0001보다 작은지를 확인한다. 그 소스 코드를 소개하겠다.

closeTo: num
    "are these two numbers close?"
    num isNumber ifFalse: [^[self = num] ifError: [false]].
    self = 0.0 ifTrue: [^num abs < 0.0001].
    num = 0 ifTrue: [^self abs < 0.0001].
    ^self = num asFloat
        or: [(self - num) abs / (self abs max: num abs) < 0.0001]

Scaled Decimal에 관하여. Scaled Decimals는 정확한 부동 소수점 수가 절대적으로 필요할 때 해결책이다. 이들은 정확수(exact number)로서 당신이 예상한 행위를 보인다.

0.1s2 + 0.2s2 = 0.3s2
    → true

이제 아래의 행을 실행하면 표현식이 같지 않음을 확인할 것이다.

(0.1 asScaledDecimal: 2) + (0.2 asScaledDecimal: 2) = (0.3 asScaledDecimal: 2)
    → false

차이가 뭘까? 가령, 0.1s2를 실행하면 처음부터 분수가 생성되므로 0.1s2 asFraction은 1/10을 리턴한다. AsScaledDecimal: 메시지는 또 다른 행위를 가진다. (0.1 asScaledDecimal: 2)는 float 0.1 (0.1 asScaledDecimal: 2)와 정확히 동일한 수를 표현하고, asFraction은 0.1 asFraction 값을 리턴한다. 0.1+0.2=0.3은 false를 리턴하므로 당연히 이 표현식의 scaled decimal은 false를 리턴할 것으로 예상할 것이다.

Float 분해하기

위의 덧셈에 수반되는 연산을 이해하기 위해서는 floats가 컴퓨터 내에서 내부적으로 어떻게 표현되는지를 알아야 한다. Pharo의 Float 포맷은 대부분 컴퓨터에서 널리 사용되는 표준, IEEE 754-1985 64비트 배정도(double precision)다 (상세한 정보는 http://en.wikipedia.org/wiki/IEEE_754-198를 참고). 해당 포맷을 이용해 Float은 아래 공식에 의해 밑이 2로 표현된다.

• 부호는 1 비트로 표현된다.
• 지수는 11 비트로 표현된다.
• 가수(mantissa)는 밑이 2인 분수로, 소수점 앞에 1이 따라오고 fraction point 다음에 52 개 이진 숫자로 구성된다. Pharo에서 가수를 얻기 위한 메서드는 Float>>significand이다. 이번 장에서 몇 가지 예를 제시한다.

예를 들어, 일련의 52 비트는:

0110010000000000000000000000000000000000000000000000

가수가 다음과 같다는 뜻이며,

1.0110010000000000000000000000000000000000000000000000

이는 아래 분수를 표현하기도 한다.

가수 값은 그에 따라 일반 숫자에 대해 1(포함)과 2(제외) 사이에 해당한다.

1 + ((1 to: 52) detectSum: [:i | (2 raisedTo: i) reciprocal]) asFloat
    → 1.9999999999999998

Float 빌드하기. 그러한 가수를 구성해보도록 하자.

(#(0 2 3 6) detectSum: [:i | (2 raisedTo: i) reciprocal]) asFloat.
    → 1.390625

이제 23으로 곱하여 null이 아닌 지수를 얻자.

(#(0 2 3 6) detectSum: [:i | (2 raisedTo: i) reciprocal]) asFloat*(2 raisedTo: 3).
    → 11.125

아니면 timesTwoPower 메서드를 이용한다.

(#(0 2 3 6) detectSum: [:i | (2 raisedTo: i) reciprocal]) asFloat timesTwoPower: 3.
    → 11.125

Pharo에서는 이러한 정보를 검색할 수가 있다.

11.125 sign.
    → 1

11.125 significand. 
    → 1.390625

11.125 exponent.
    → 3

Pharo에는 정규화된 가수를 직접 처리하는 메시지가 없다. 대신 52 비트를 좌측으로 쉬프팅한 다음 가수를 정수로서 처리하는 것이 가능하다. 이를 행하는 데에는 한 가지 합당한 이유가 있다. 산술이 정확하기 때문에 Integer에서 연산하기가 더 수월하다는 점이다. 결과는 앞에 붙은 1을 포함하므로 일반 숫자에 대해 53 비트 길이어야 한다 (이것이 float precision이다).

11.125 significandAsInteger
    → 6262818231812096

11.125 significandAsInteger printStringBase: 2.
    → '10110010000000000000000000000000000000000000000000000'

'10110010000000000000000000000000000000000000000000000' size
    → 53

11.125 significandAsInteger highBit.
    → 53

Float precision.
    → 53

Float에 대한 내부 표현에 상응하는 정확한 분수를 검색할 수도 있다.

11.125 asTrueFraction.
    → (89/8)

(#(0 2 3 6) detectSum: [:i | (2 raisedTo: i) reciprocal])*(2 raisedTo: 3).
    → (89/8)

정확한 입력을 검색할 때까지 우리는 Float으로 추가한다. 결국 Float 연산은 정확한가? 음, 아니다, 2 제곱을 분모로 가진 분수와 분자에 몇 비트만 실험을 해봤을 뿐이다. 이러한 조건 중 하나라도 충족되지 않으면 우리는 숫자에 대한 정확한 Float 표현을 찾지 못할 것이다. 예를 들자면, 1/5를 이진 숫자의 유한수(finite number)로는 표현하는 것이 불가능하다. 따라서 0.1과 같은 소수(decimal fraction)는 위의 표현식으로는 정확히 표현할 수 없다.

(1/5) asFloat = (1/5).
    → false

(1/5) = 0.2
    → false

1/5의 분수 비트(fractional bits), 가령 2r1/2r101는 어떻게 얻는지 상세히 살펴보자. 이를 위해 먼저 나눗셈을 열거해야 한다.

우리 눈에 보이는 것은 하나의 사이클로, 4회의 유클리드(Euclidean) 나눗셈마다 몫으로 2r0011, 나머지 1을 얻는다. 즉, 밑이 2인 1/5 를 표현하기 위해서는 해당 비트 패턴의 무한 series가 필요하다는 의미다. (1/5)를 Float로 변환하기 위해 Pharo가 처리한 방식을 살펴보자.

(1/5) asFloat significandAsInteger printStringBase: 2.
    → '11001100110011001100110011001100110011001100110011010'

(1/5) asFloat exponent.
    → -3

마지막 비트 001이 010로 올림된 것만 제외하면 우리가 예상한 비트 패턴이다. 이는 Float의 기본 올림/내림(rounding) 모드로서, 가장 가까운 짝수로 올림/내림한다. 이제 머신이 0.2를 부정확하게 표현한 이유를 이해할 수 있을 것이다. 이것은 0.1에 대한 동일한 가수로, 그 지수는 -4다.

0.2 significand
    → 1.6

0.1 significand
    → 1.6

0.2 exponent
    → -3

0.1 exponent
    → -4

이제 0.1 + 0.2로 진입하는데, (1/10)+(1/5)를 정확히 얻지는 못했다. 대신 아래의 결과를 얻었다.

0.1 asTrueFraction + 0.2 asTrueFraction.
    → (10808639105689191/36028797018963968)

이것이 전부가 아니다... 위의 분수에서 비트 패턴을 살펴보고, 피트 패턴의 span을 확인해 보면 가장 큰 비트의 위치가 1(가장 왼쪽)로 설정되고 최하위 비트의 위치는 1(가장 오른쪽)로 설정된다.

10808639105689191 printStringBase: 2.
    → '100110011001100110011001100110011001100110011001100111'

10808639105689191 highBit.
    → 54

10808639105689191 lowBit.
    → 1

36028797018963968 printStringBase: 2.
    → '10000000000000000000000000000000000000000000000000000000'

분모는 예상한 대로 2 제곱이지만 분자를 보관하기 위해서는 54 비트의 정밀도가 필요하다... Float은 53 비트만 제공한다. Float 표현에 들어맞기에는 또 다른 올/내림 오류가 존재할 것이다.

(0.1 asTrueFraction + 0.2 asTrueFraction) asFloat = (0.1 asTrueFraction + 0.2 asTrueFraction).
    → false

(0.1 asTrueFraction + 0.2 asTrueFraction) asFloat significandAsInteger.
    → '10011001100110011001100110011001100110011001100110100'

10진법 표현이 Float 표현으로 변환된 것을 포함해 무슨 일이 일어났는지 요약하자면 다음과 같다.

(1/10) asFloat 0.1 inexact (rounded to upper; 위로 올림)

(1/5) asFloat 0.2 inexact (rounded to upper; 위로 올림)

(0.1 + 0.2) asFloat · · · inexact (rounded to upper; 위로 올림)

3개의 부정확한 연산이 발생했고, 아쉽게도 3개의 올/내림 연산이 올림되어 전멸되기보다는 더 축적되었다. 반면 0.3의 해석은 asFloat으로서 하나의 올/내림 오류(3/10)를 야기한다. 이제 0.1+0.2=0.3을 기대할 수 없는 이유를 이해할 것이다.

연습으로 1.3*1.3≠1.69가 되는 이유를 보이겠다.

Floats를 이용하면 출력이 부정확해진다

위의 예제에서 알게 된 가장 큰 함정은 0.1이 마치 정확한 수치인 것처럼 '0.1'로 출력되지만 사실은 정확하지 않다는 것이다. printString이 내부적으로 사용하는 absPrintExactlyOn:base: 라는 이름이 약간은 혼동스러운데, 정확히 출력하지 않고 다시 읽었을 때 동일한 Float으로 올/내림될 가장 짧은 10진법 표현을 출력한다 (Pharo는 10진법 표현을 항상 가장 가까운 Float으로 변환한다).

정확한 출력을 위해 존재하는 또 다른 메시지, printShowingDecimalPlaces:를 대신 사용할 필요가 있겠다. 모든 무한 Float은 무한의 10진 숫자로 된 10진법 표현을 갖는다 (5 제곱으로 된 분모에 분자를 곱하면 숫자를 얻게 될 것이다). 아래를 살펴보자.

0.1 asTrueFraction denominator highBit.
    → 56

분수의 분모가 255이며, 0.1의 내부적 표현을 정확히 출력하기 위해서는 소수점 다음에 55개의 10진 숫자가 필요하다는 의미다.

0.1 printShowingDecimalPlaces: 55.
    → '0.1000000000000000055511151231257827021181583404541015625'

그리고 아래를 이용해 숫자를 검색할 수 있다.

0.1 asTrueFraction numerato*(5 raisedTo: 55).
    → 1000000000000000055511151231257827021181583404541015625

아래를 이용하면 결과를 확인할 수 있다.

1000000000000000055511151231257827021181583404541015625/(10 raisedTo: 55) = 0.1 asTrueFraction
    → true

위에서 확인할 수 있듯이 머신에서 표현되는 내용의 정확한 표현을 출력하기란 가능한 일이지만 상당히 번거롭다. 의심이 간다면 1.0e100을 정확하게 출력해보라.

Float 올/내림도 부정확하다

float 동등성에 대한 악명이 높긴 하나 float의 다른 측면들에도 주의를 기울여야 한다. 아래 예제를 이용해 요점을 설명하겠다.

2.8 truncateTo: 0.01
    → 2.8000000000000003

2.8 roundTo: 0.01
    → 2.8000000000000003

2.8 truncateTo:0.01이 2.8을 리턴하지 않고 2.8000000000000003을 리턴한다는 것은 놀랍지만 틀린 답은 아니다. 이는 truncateTo: 와 roundTo: 가 floats에서 여러 개의 연산을 실행하기 때문인데, 부정확한 숫자에서 부정확한 연산을 실행하면 위에서 확인한 것과 같이 누적 올/내림 오류가 발생할 수 있으며, 위의 결과도 이로 인한 것이다.

정확히 연산을 실행한 후 가장 가까운 Float으로 올/내림한다 하더라도 초기에 2.8과 0.01의 부정확한 표현 때문에 결과는 여전히 부정확하다.

(2.8 asTrueFraction roundTo: 0.01 asTrueFraction) asFloat
    → 2.8000000000000003

0.01 대신 0.01s2 를 이용하면 예제가 제대로 작동하는 듯 보인다.

2.80 truncateTo: 0.01s2
    → 2.80s2

2.80 roundTo: 0.01s2
    → 2.80s2

하지만 이는 순전히 운이며, 2.8이 부정확하다는 사실만으로 아래와 같이 갑작스러운 상황을 야기하기엔 충분하다.

2.8 truncateTo: 0.001s3.
    → 2.799s3

2.8 < 2.800s3.
    → true

Float의 세계에서 자르기(truncating)는 극도로 불안정하다. 그나마 ScaledDecimal을 올/내림에 이용하면 그러한 불일치를 야기할 가능성이 낮으나, 마지막 숫자를 대상으로 할 때는 이마저도 불안정하다.

부정확한 표현 갖고 놀기

마무리를 짓기 위해 부정확한 표현을 조금 더 갖고 놀아보자. 여러 숫자들 간 차이를 확인해보자.

{
((2.8 asTrueFraction roundTo: 0.01 asTrueFraction) - (2.8 predecessor)) abs -> -1.
((2.8 asTrueFraction roundTo: 0.01 asTrueFraction) - (2.8)) abs -> 0.
((2.8 asTrueFraction roundTo: 0.01 asTrueFraction) - (2.8 successor)) abs -> 1.
} detectMin: [:e | e key ]

    → 0.0->1

아래 표현식은 0.0->1을 리턴하며 이는 (2.8 asTrueFraction roundTo: 0.01 asTrueFraction) asFloat = (2.8 successor) 을 뜻한다.

하지만 아래를 기억하라.

(2.8 asTrueFraction roundTo: 0.01 asTrueFraction) ∼= (2.8 successor)

(2.8 asTrueFraction roundTo: 0.01 asTrueFraction)에 가장 가까운 Float은 (2.8 successor)라고 해석되어야 한다.

한계를 확인하고 싶다면 아래를 시도해보라.

((2.8 asTrueFraction roundTo: 0.01 asTrueFraction) - (2.8 successor asTrueFraction))
    asFloat
    → -2.0816681711721685e-16

요약

Floats는 광범위한 10진 값을 지원하는 실수의 근사치에 해당한다. 본 장에서는 다음과 같은 요점을 살펴보았다.

• float을 비교 시 =를 절대 사용하지 말라 (예: (0.1+0.2)=0.3은 false를 리턴한다)
• 대신 closeTo:를 사용하라 (예: (0.1+0.2) closeTo: 0.3은 true를 리턴한다)
• 부동 소수점 수는 밑이 sign x mantisa(가수) x 2^{exponent(지수)} (예: 1.2345=12345x10^-4)로 표현된다
• float로 올림(rounding up)하거나 자를 경우 truncateTo: 와 roundTo: 가 항상 작동하는 것은 아니다 (예: 2.8 roundTo: 0.02은 2.800...003을 리턴한다)

floats에 관해서는 알아야 할 사항들이 아직 더 많으므로 충분히 학습했다면 아래 링크를 확인해보는 것도 좋은 생각이다. "What Every Computer Scientist Should Know About Floating-Point Arithmetic" ( http://www.validlab.com/goldberg/paper.pdf ).