DeepintoPharo:Chapter 15

제 15 장 소수(little numbers) 탐구하기

소수(little numbers) 탐구하기

우리는 항상 숫자를 조작한다. 따라서 이번 장에서는 정수가 이진수 표현으로 매핑되는 방식을 간단히 살펴보고자 한다. 상자를 열고 언어 구현자 관점을 취해 작은 정수들이 어떻게 표현되는지 기꺼이 탐구할 것이다.

가장 먼저 디지털 세계의 기본인 수학을 몇 가지 상기시키고자 한다. 이후 정수, 특히 작은 정수가 어떻게 인코딩되는지 살펴볼 것이다. 시간이 지나면서 사람들이 잊어버리곤 하는 단순한 지식이니만큼 우리는 이를 상기시키는 데에 목표를 둔다.

2 제곱과 숫자

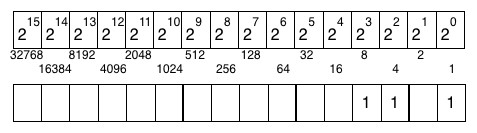
단순한 수학 문제부터 시작해보자. 디지털 세계에서 정보는 2의 제곱으로 인코딩된다. 새로운 건 없다. 스몰토크에서 숫자를 거듭제곱하는 것은 숫자로 raisedTo: 메시지를 전송하여 이루어진다. 몇 가지 예를 들어보겠다. 그림 15.1은 2 제곱을 보여준다.

2 raisedTo: 0
    → 1
2 raisedTo: 2
    → 4
2 raisedTo: 8
    → 256

2제곱의 시퀀스를 이용해 숫자를 인코딩할 수 있다. 예를 들어, 13이란 숫자는 어떻게 인코딩할까? 24=16이므로 24보다 클 수는 없다. 따라서 8+4+1, 23+22+20이어야 한다. 이제 2곱을 그림 15.2에 표시된 시퀀스로 정렬하면 13이 1101로 인코딩됨을 볼 수 있다. 따라서 2제곱의 시퀀스를 이용해 숫자를 인코딩할 수 있는 것이다. 시퀀스의 요소는 비트라고 부른다. 13은 4비트로 인코딩되고, 1 ∗ 23+1∗ 22+0∗ 21+1∗ 20에 해당한다. 이러한 비트의 시퀀스는 숫자에 대한 이진수 표기법을 나타낸다. 최상위 비트는 비트 시퀀스에서 가장 왼쪽에, 최하위 비트는 가장 오른쪽에 위치한다 (20이 가장 오른쪽 비트).

이진수 표기법

스몰토크는 숫자를 다른 밑(base)으로 표현하기 위한 구문을 갖고 있다. 2r1101으로 작성하면 2는 밑 또는 기수를 뜻하고 여기서는 2에 해당하며, 나머지는 이를 밑으로 표현된 숫자를 나타낸다. 2r01101 또는 2r0001101으로 작성할 수도 있는데, 해당 표기법은 최하위 비트가 가장 오른쪽에 위치하는 규칙을 따르기 때문이다.

2r1101
    → 13
13 printStringBase: 2
    → '1101'
Integer readFrom: '1101' base: 2
    → 13

마지막 두 메시지, printStringBase: 와 readFrom:base: 는 후에 살펴보겠지만 음수의 내부적 인코딩을 잘 처리하지 못한다. -2 printStringBase: 2는 -10을 리턴하지만 이는 내부적 숫자 표현(2의 보수로 알려진)이 아니다. 이러한 메시지들은 그저 주어진 밑으로 숫자를 출력/읽을 뿐이다.

기수 표기법을 이용해 여러 밑으로 숫자를 명시할 수도 있다. 십진수로 작성된 15는 (10r15) 15를 리턴하는 반면 밑이 16인 15는 아래 표현식에서 보여주듯 16+5=21을 리턴한다.

10r15
    → 15
16r15
    → 21

비트 쉬프팅(bit shifting)은 2 제곱을 곱하는 것이다

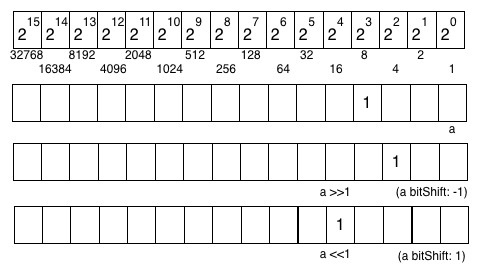
정수는 비트의 시퀀스로서 표현되므로, 모든 비트를 주어진 양부터 쉬프팅한다면 또 다른 정수를 얻게 된다. 비트의 쉬프팅은 2의 곱셈/나눗셈을 실행하는 것과 같다. 그림 15.3은 이러한 요점을 보여준다. 스몰토크는 비트를 쉬프팅하는 세 개의 메시지를 제공하는데, >> aPositiveInteger, <<aPositiveInteger, 그리고 bitShift: anInteger가 그것들이다. >> 는 수신자 나누는 반면 << 는 2 제곱으로 곱한다.

아래 예제들을 통해 사용 방법을 소개하겠다.

2r000001000
    → 8
2r000001000 >> 1 "we divide by two"
    → 4
(2r000001000 >> 1) printStringBase: 2
    → '100'
2r000001000 << 1 "we multiply by two"
    → 16

bitShift: 메시지는 >> 와 <<에 동일하지만 방향을 전환 시 음의 정수와 양의 정수를 사용한다. 양의 인자는 <<와 동일한 행위를 제공하고, 수신자를 2제곱으로 곱한다. 음의 인자는 >>와 유사하다.

2r000001000
    → 8
2r000001000 bitShift: -1
    → 4
2r000001000 bitShift: 1
    → 16

물론 한 번에 1 비트 이상 쉬프팅도 가능하다.

2r000001000
    → 8
2r000001000 >> 2 "we divide by four"
    → 2
(2r000001000 >> 2) printStringBase: 2
    → '10'
2r000001000 << 2 "we multiply by four"
    → 32

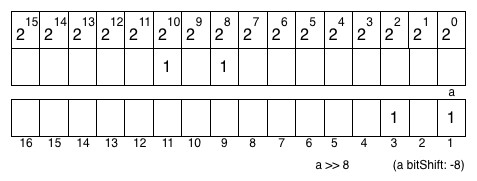
앞의 예제들은 1 비트 또는 2 비트로 된 숫자의 비트 쉬프팅을 보여주는데, 이 수준에서는 제약이 없다. 완전한 비트의 시퀀스는 아래와 그림 15.4의 2r000001100과 같이 쉬프팅될 수 있다.

(2 raisedTo: 8) + (2 raisedTo: 10)
    → 1280
2r010100000000
    → 1280
2r010100000000 >> 8
    → 5

지금까진 특별한 내용이 없다. 기본 수학 수업에서 배웠겠지만 항상 산을 오르기 전에는 언덕부터 걷는 연습이 필요하기 때문에 소개한 내용이다.

비트 조작과 접근

Pharo는 비트 조작을 위한 일반 부울 연산을 몇 가지 제공한다. 따라서 bitAnd:, bitOr:, bitXor: 과 같은 메시지들을 number로 전송할 수 있다. 그들은 연관된 Boolean 연산을 비트별로 적용할 것이다.

2r000001101 bitAnd: 2r01
    → 1
2r000001100 bitAnd: 2r01
    → 0
2r000001101 bitAnd: 2r1111
    → 1101

bitAnd: 는 숫자의 일부를 선택하는 데에 사용되기도 한다. 가령, bitAnd: 2r111 는 첫 3개의 비트를 선택한다.

2r000001101 bitAnd: 2r111
    → 5
2r000001101 bitAnd: 2r0
    → 0
2r0001001101 bitAnd: 2r1111
    → 13 "1101"
2r000001101 bitAnd: 2r111000
    → 8 "1000"
2r000101101 bitAnd: 2r111000
    → 40 "101000"

bitShift: 와 함께 bitAnd: 를 사용하면 숫자의 일부를 선택할 수 있다. 세 개의 숫자를 10 비트에서 인코딩한다고 가정해보자. 즉 3 비트에서 하나의 숫자를 인코딩하고 (0과 7 사이 숫자-ZZZYYYYXXX에서 XXX로 표기), 하나의 숫자는 4 비트에서 인코딩되며 (0과 15 사이 숫자-ZZZYYYYXXX에서 YYYY로 표기), 마지막으로 세 번째 숫자는 3비트에서 인코딩되고 ZZZYYYYXXX에서 ZZZ로 표기된다고 가정하자. 아래 표현식을 이용하면 쉽게 조작이 가능하다. 두 번째 숫자로 접근할 때는 단순히 bitShift: 만 이용해선 불가능한데, 세 번째 숫자가 여전히 존재할 것이기 때문이다. (2r1001111001bitShift: -3)는 79를 리턴하는데 우리가 얻고자 하는 값은 15다. 해결책은 세 번째 숫자를 삭제하기 위해 bitAnd: 를 사용하고 bitShift:를 실행하거나, bitShift:를 실행하고 세 번째 숫자를 삭제하는 방법이 있다. BitAnd: 인자는 인코딩의 오른쪽 부분을 선택하도록 조정되어야 한다.

(2r1001111001 bitShift: -3)
    → 79
(2r1001111001 bitAnd: 2r0001111000)
    → 120
(2r1001111001 bitAnd: 2r0001111000) bitShift: -3
    → 15
(2r1001111001 bitShift: -3) bitAnd: 2r0001111
    → 15

비트 접근. 스몰토크는 비트 정보로 접근하도록 해준다. BitAt: 메시지는 주어진 위치에 비트 값을 리턴한다. 이는 컬렉션의 색인이 1부터 시작되는 스몰토크 규칙을 따른다.

2r000001101 bitAt: 1
    → 1
2r000001101 bitAt: 2
    → 0
2r000001101 bitAt: 3
    → 1
2r000001101 bitAt: 4
    → 1
2r000001101 bitAt: 5
    → 0

시스템 자체로부터 학습한다면 흥미로울 것이다. Integer 클래스에 bitAt: 메서드의 구현을 살펴보자.

Integer>>bitAt: anInteger
    "Answer 1 if the bit at position anInteger is set to 1, 0 otherwise.
    self is considered an infinite sequence of bits, so anInteger can be any strictly positive
        integer.
    Bit at position 1 is the least significant bit.
    Negative numbers are in two-complements.

    This is a naive implementation that can be refined in subclass for speed"

    ^(self bitShift: 1 - anInteger) bitAnd: 1

정수 - 1에서부터 (따라서 1 - anInteger) 오른쪽으로 쉬프팅하고, bitAnd: 를 이용해 위치에 1이 있는지 0이 있는지를 알게 된다. 2r000001101를 갖고 있다고 가정할 때, 2r000001101 bitAt: 를 실행하면 4부터 쉬프팅되어 해당 비트를 선택하는 bitAnd: 1을 실행할 것이다 (예: 1에 있을 경우 1을 리턴하고, 그 외의 경우 0을 리턴하므로 그 값이 되겠다). bitAnd: 1 을 실행하는 것은 최하위 비트에 1이 있는지 알려주는 것과 동일하다.

다시 말하지만 사실상 특별한 내용은 없으며 모두 기억하고 있는 것을 상기시키는 데에 목적을 둔다. 이제 숫자가 2의 보수를 이용해 Pharo에서 내부적으로 인코딩되는 방법을 살펴볼 것이다. 먼저 10의 보수를 이해한 후 2의 보수를 살펴보겠다.

숫자에 대한 10의 보수

2의 보수를 완전히 이해하기 위해서는 그것이 십진수와 어떻게 작용하는지 살펴보는 편이 흥미롭다. 10의 보수에 대한 사용을 분명히 보여주는 예는 없지만 여기서 보여주고픈 요점은 보수가 덧셈을 뺄셈으로 대체하는 것이란 사실이다 (예: A의 보수를 B로 더하는 것은 B에서 A를 제하는 것과 같다).

양의 십진 정수 n에 대한 10의 보수는 10 의 (k)제곱에서 마이너스 n인데 여기서 k는 n의 십진 표현으로 된 자릿수를 의미한다. Complement10(n) = 10k− n. Complement10(8) = 101− 8, Complement10(1968) = 104− 1968 = 8032를 예로 들 수 있겠다.

이는 아래와 같은 방법으로 계산할 수 있다.

1. 숫자의 각 자릿수 d를 9-d로 대체하고,
2. 결과 숫자에 1을 추가하라.

예제. 1968에 대한 10의 보수는 9-1, 9-9, 9-6, 9-8+1로, 예를 들자면 8031+1, 가령 8032가 된다. 규칙 2를 이용해 9-1, 9-9, 9-6, 10-8를 계산하므로 8032를 예로 들 수 있다. 따라서 1968에 대한 10의 보수는 8032가 된다. 사실 1968+8032=10000=105이다. 따라서 위의 정의를 올바로 따르면 8032는 10000-1968의 결과가 된다.

190680에 대한 10의 보수는 9-1, 9-9, 9-0, 9-6, 9-8, 9-0+1, 가령 809319+1, 따라서 809320가 된다. 확인해보자. 190680+809320=10000000.

숫자에 대한 10의 보수를 계산하기 위해서는 각 자릿수마다 9-d를 실행하여 결과에 추가하는 것만으로 충분하다.

일부 서적에서는 10의 보수를 계산하는 또 다른 방법을 제시한다. (1) 숫자 오른쪽 끝의 모든 0은 0으로 계속 유지된다. (2) 숫자의 오른쪽에서 0이 아닌 자릿수 d는 10-d로 대체된다. (3) 그 외 다른 자릿수 d는 9-d로 대체된다.

컴퓨터 과학자들은 첫 번째 방법을 아마도 선호할 것인데, 좀 더 일반적일 뿐더러 1을 추가하는 것이 다른 테스트를 만드는 것보다 덜 번거롭기 때문이다.

뺄셈 작용

보수 기법의 핵심은 뺄셈을 덧셈으로 전환한다는 데에 있다. 확인해보자.

예제. 8-3=5 뺄셈을 실행하길 원한다고 가정하자. 10의 보수를 이용해 뺄셈을 덧셈으로 변형할 것이다. 3에 대한 10의 보수는 9-3+1=7이다. 8에 7을 더해 15를 얻는다. 덧셈에서 얻은 carry를 버리고(drop) 5를 얻는다. 사실 8-3=8-(10-7)=8+7-10=15-10=5가 이루어진다.

이제 98-60을 계산해보자. 60에 대한 10의 보수는 9-6, 9-0으로, 가령 39+1, 즉 40이 된다. 98 − 60 = 98 + 40 − 100 = 138 − 100 = 38. 따라서 98 − 60 = 98 + 40 = (1)38 이라 말할 수 있으며, carry를 버린다.

이제 −98 + 60 를 실행하기 위해 98에 대한 10의 보수를 계산하고 합을 계산한 후 합에 대한 10의 보수를 계산하고 반전(negate)하는데, −98 + 60는 2 + 60 = 62가 되고, 62에 대한 10의 보수는 38 이 되므로 −98 + 60 = −38가 된다.

다시 살펴보기. 숫자를 10의 보수로 대체하는 것은 a − b = a − (10 − c)를 기반으로 하는데, 여기서 10 = b + c 를 충족한다. 결과가 81443인 아래 표현식 190680 − 109237 을 생각해보자. 10의 보수는 109237 역시 999999-890762 또는 1000000-890763과 동일하며 890763가 109237에 대한 10의 보수라는 사실을 이용한다.

109237 = 999999 - 890762
109237 = 999999 - 890762 (+ 1 - 1)
109237 = 1000000 - 890762 - 1

이제 첫 번째 뺄셈은 아래와 같이 표현된다.

190680 - 109237
= 190680 - (1000000 - 890762 - 1)
= 190680 - 1000000 + 890762 + 1
= 190680 + 890762 + 1 - 1000000
= 1081443 - 1000000
= 81443

음수

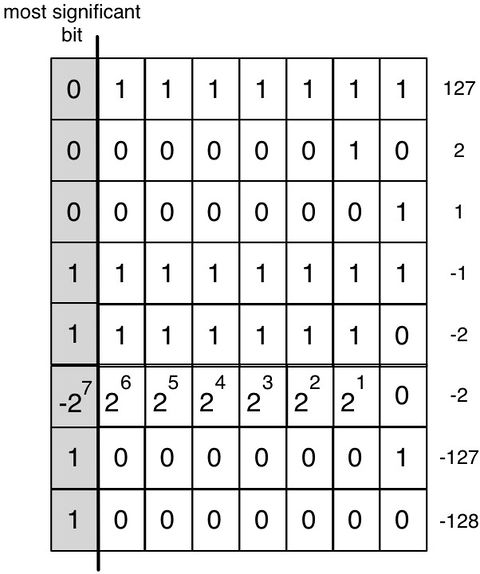
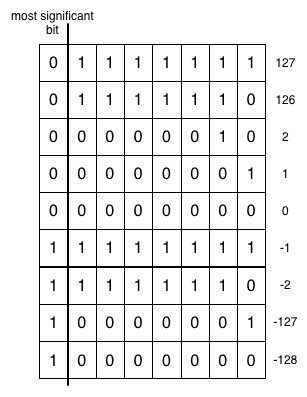
음수의 값은 간단히 알 수 있다. 본 장 앞에서 설명했듯이 이진수 표현에 의해 주어진 모든 2제곱을 합하면 된다. 음수 값을 얻는 것도 이제 꽤 간단해졌다. Sign bit를 음으로 계수하고, 나머지는 모두 양으로 계수한다는 점만 제외하면 앞과 동일하다. Sign bit는 최상위 비트로서, 가장 큰 수를 나타내는 비트이다(그림 15.5 참고). 예를 들어 8 비트 표현에서 이는 weight 27과 연관된 비트일 것이다.

이를 설명해보겠다. -2는 8 비트에서 1111 1110으로 인코딩되어 표시된다. 비트 표현으로부터 값을 얻기 위해서는 −27+ 26+25+ 24+ 23+ 22+ 21+ 0 ∗ 20를 더하여, −128 + 64 + 32 + 16 + 8 + 4 + 2가 되고 결국 -2를 얻는다.

-69은 8비트에서 1011 1011로 표현된다. 비트 표현에서 값을 얻기 위해선 −27+ 0 ∗ 26+ 25+ 24+ 23+ 0∗22+ 21+ 20를 합해 −128 + 32 + 16 + 8 + 2 + 1 가 되고 결국 −69를 얻는다.

같은 규칙에 따라 -1 값이 그림 15.5에 설명한 값인지 확인하라.

비트를 세어보자. 8 비트 표현에서 우리는 0을 255의 음의 정수 또는 -128부터 64 + 32 + 16 + 8 + 4 + 2 + 1 127까지 인코딩할 수 있다. 사실 우리는 -1*27에서 27-1로 인코딩할 수도 있다. 좀 더 일반적으로 N 비트에서는 -1*2N-1에서 2N-1-1 정수 값으로 인코딩이 가능하다.

숫자에 대한 2의 보수

이제 모든 퍼즐 조각은 손에 있다.양수와 음수를 인코딩하는 방법을 알고, 뺄셈을 덧셈으로 바꾸기 위해 보수를 사용하는 법도 알고 있다. 이제 2의 보수를 이용해 숫자를 반전하고 뺄셈을 실행해보자.

2의 보수는 부호가 있는(signed) 정수를 표현하기 위한 일반적인 메서드이다. 사용 시 이점으로는, 비연산자의 부호를 확인하거나 2의 보수가 0에 대해 하나의 표현만 갖는지 (음의 제로를 피하기 위해) 확인할 필요 없이 덧셈과 뺄셈이 구현된다는 데에 있다. 2의 보수를 이용해 인코딩된 부호의 숫자를 추가할 때에는 어떤 특별한 처리도 필요로 하지 않는다. 결과의 부호가 자동으로 결정되기 때문이다. 양수에 대한 2의 보수는 해당 숫자의 음수 형태를 나타낸다.

10의 보수는, 베이스 시스템에서 이용 가능한 최대수로 된 각 digit와 십진수로 된 9의 차(difference)에 1을 더하면 계산할 수 있음을 보여준다. 이제 이진수의 경우, 최대값은 1이 된다. 1-0=1과 1-1=0이란 사실 때문에 숫자에 대한 2의 보수를 계산하는 것은 1의 보수(1's)를 0의 보수(0's)로, 혹은 그 반대로 뒤집어(flipping) 1을 더하는 것과 정확히 동일하다.

숫자 2를 살펴보자. 그림 15.6에서와 같이 2는 8 비트에서 000000010로 인코딩되고, -2는 11111110로 인코딩된다. 뒤집은 000000010은 11111101이고 그에 1을 더하면 11111110을 얻는다. -2(11111110)와 126(01111110)의 차는 정수 부호를 전달하는 최상위 비트에 의해 주어진다.

Pharo에서 아래 표현식을 시도하고 실험해보라. 우리는 직접 역전(direct inversion; bitwise NOT)을 계산 후 1을 더한다. Bitwise NOT은 어떤 1이든 0으로 바꾸고, 0은 1로 바꾼다. 숫자의 비트 표현을 얻는 데에 bitString을 사용할 수도 있다. 출력된 결과의 길이를 확인하면 32대신 31비트임을 눈치챌 것이다. 이는 Pharo와 스몰토크 구현에서는 작은 정수가 특별히 인코딩되고, 해당 인코딩은 1 비트를 필요로 하기 때문이다.

2 bitString
    '0000000000000000000000000000010'
2 bitInvert bitString
    '1111111111111111111111111111101'
(2 bitInvert + 1) bitString
    '1111111111111111111111111111110'
-2 bitString
    '1111111111111111111111111111110'

음수에 대한 2의 보수는 다음 표현식에 의해 표시되는 해당 양수 값이다. -2에 대한 2의 보수는 2다. 먼저, 직접 역전(bitwise NOT)을 계산하고 1을 더한다.

-2 bitString
    → '1111111111111111111111111111110'
-2 bitInvert bitString
    → '0000000000000000000000000000001'
(-2 bitInvert + 1) bitString
    → '0000000000000000000000000000010'
2 bitString
    → '0000000000000000000000000000010'

숫자를 반전하고 2의 보수를 계산하면 동일한 이진수 표현을 제공함을 알 수 있다.

(2r101 bitInvert + 1) bitString
    returns '1111111111111111111111111111011'
2r101 negated bitString
    returns '1111111111111111111111111111011'

한 가지 예외가 있다. 주어진 비트 번호에서, 즉 그림 15.6에서처럼 비트 8이라고 가정하면, 우리는 음수를 계산하지만 가장 큰 음수를 제하고는 숫자에 대한 2의 보수(모든 비트를 뒤집고 1을 추가)를 계산한다. 8비트 표현에서 가장 큰 음수는 -128(1000 0000)으로 역전하면 (0111 1111)이며, 1을 더하면 (1000 0000)이 된다. 8비트 부호가 있는 규칙에서 128를 인코딩할 수는 없다. 여기서 carry는 sign bit에 의해 "먹힌다(eaten)".

뺄셈. 숫자를 어떤 숫자로 빼기 위해서는 두 번째 숫자에 대한 2의 보수를 첫 번째 숫자로 추가하면 된다.

가령 110110-101을 계산하려면 101에 대한 2의 보수를 계산해 추가한다. 110110과 111011을 더하여 110001을 얻는다. 따라서 54-5=49가 올바르겠다.

110110 - 101
  110110
+ 111011
----------
  110001

Pharo에서 테스트해보자.

(2r110110 - 2r101) bitString
    → '0000000000000000000000000110001'
(2r110110 bitString)
    → '0000000000000000000000000110110'
2r101 bitString
    → '0000000000000000000000000000101'
2r101 negated bitString
    → '1111111111111111111111111111011'

8 비트만 사용해 덧셈을 제시하면 아래와 같은 모습이 발생한다.

carry 1111111
      00110110
+     11111011
----------------
      00110001

overflowing carry가 버려졌음을 주목하라.

이제 결과가 음수인 경우 역시 잘 처리된다. 예를 들어, 15-35를 계산하고 싶다면 -20를 얻어야 하고 바로 그 값을 얻게 될 것이다. 15가 0000 1111로 인코딩되고 35은 0010 0011로 인코딩되는 모습을 살펴보자. 35에 대한 2의 보수는 1101 1101이다.

      0011111 (carry)
      0000 1111
      1101 1101
-----------------
  1111111101100

결과적으로 -20을 얻는다.

Pharo에서 SmallIntegers

스몰토크의 작은 정수는 31 비트에서 2의 보수 산술을 이용한다. N-비트의 2의 보수 기수법(two's complement numeral system)은 −1 ∗ 2N−1부터 2N−1− 1범위의 모든 정수를 표현 가능하다. 따라서 31 비트의 경우 스몰토크 시스템 작은 정수 값은 -1 073 741 824 부터 1 073 741 823 범위에 해당한다. 스몰토크에서는 정수가 특수 객체이며, 그 표기 시 1비트가 소모되므로 32비트에선 작고 부호가 있는 정수에 대해 31비트를 갖고 있음을 기억하라. 물론 자동 강제변환(automatic coercion)도 갖고 있으므로 최종 프로그래머에겐 문제가 되지 않는다. 본문에서는 언어 구현의 관점을 취하고 있다. 해당 비트를 확인해보자 (이제 다루어도 될 시기다).

SmallInteger 최대값 인코딩. Pharo의 작은 정수는 31비트 상에서 인코딩되고 (내부 표현에 1비트가 필요하므로), 최소 (small integer) 음의 정수는 SmallInteger maxVal negated -1이다. 여기서는 가장 큰 음의 정수에 대한 예외를 살펴보겠다.

"We negate the maximum number encoded on a small integer"
SmallInteger maxVal negated
    → -1073741823
"we still obtain a small integer"
SmallInteger maxVal negated class
    → SmallInteger
"adding one to the maximum number encoded on a small integer gets a large positive integer"
(SmallInteger maxVal + 1) class
    →LargePositiveInteger
"But the smallest negative is one less than the negated largest positive small integer"
(SmallInteger maxVal negated - 1)
    → -1073741824
(SmallInteger maxVal negated - 1) class
    → SmallInteger

일부 메서드 이해하기. SmallInteger를 표현하는 데에 사용된 비트 수를 알기 위해선 아래를 평가하라.

SmallInteger maxVal highBit + 1
    returns 31

SmallInteger maxVal highBit는 양의 SmallInteger를 나타내는 데에 사용 가능한 최상위 비트를 알려주고, +1은 SmallInteger의 sign bit를 설명한다 (양수는 0, 음수는 1). 조금 더 살펴보자.

2 raisedTo: 29
    → 536870912
536870912 class
    → SmallInteger
2 raisedTo: 30
    → 1073741824
1073741824 class
    → LargePositiveInteger
(1073741824 - 1) class
    →SmallInteger
-1073741824 class
    → SmallInteger
2 class maxVal
    returns 1073741823
-1*(2 raisedTo: (31-1))
    → -1073741824
(2 raisedTo: 30) - 1
    → 1073741823
(2 raisedTo: 30) - 1 = SmallInteger maxVal
    → true

16진법

16진법을 언급하지 않고는 본 장을 완료할 수가 없을 것이다. 스몰토크에서는 이진수와 동일한 구문이 16진법에도 사용된다. 16rF는 F가 16 을 밑으로 하여 인코딩된다는 의미다.

hex메시지를 이용하면 숫자에 대한 16진 값을 얻을 수 있다. printStringHex 메시지를 이용하면 기수 표기법 없이 16진법으로 출력된 숫자를 얻는다.

15 hex
    returns '16rF'
15 printStringHex
    returns 'F'
16rF printIt
    returns 15

아래는 어떤 숫자와 그 16진 값에 동일한 결과를 열거한다.

{(1->'16r1'). (2->'16r2'). (3->'16r3'). (4->'16r4'). (5->'16r5'). (6->'16r6'). (7->'16r7').
    (8->'16r8'). (9->'16r9'). (10->'16rA'). (11->'16rB'). (12->'16rC'). (13->'16rD'). (14
    ->'16rE'). (15->'16rF')}

비트 조작을 할 때는 이진법보다 16진 표기법을 사용하는 편이 더 간결한 경우가 종종 있다. bitAnd:의 경우에는 이진수 표기법이 가독성이 더 뛰어날지 모르지만 말이다.

16rF printStringBase: 2
    returns '1111'
2r00101001101 bitAnd: 2r1111
    returns 2r1101
2r00101001101 bitAnd: 16rF
    returns 2r1101

요약

스몰토크는 내부의 작은 정수 표현에 2의 보수 인코딩을 사용하고, 내부 표현에 대해 비트 조작을 지원한다. 이는 간단한 인코딩을 이용해 알고리즘의 속도를 높이고 싶을 때 유용하다. 앞에서 살펴본 내용을 요약하자면 다음과 같다.

• 절대값은 음의 값을 인코딩하기 위해 보수를 사용한다.
• 비트를 왼쪽으로 여러 번 쉬프팅하면 비트에 2를 곱하고 그 인코딩 크기의 최대 값을 modulo 한다.
• 반대로 비트를 오른쪽으로 쉬프팅하면 비트를 2로 나눈다.
• 비트 연산은 어떤 절대값에서도 실행 가능하다.
• 보수는 덧셈을 뺄셈으로 바꾸는 데에 유용하므로 연산을 간소화한다.
• SmallInteger는 Pharo에서 31 비트에 인코딩된다.

Pharo는 원하는 만큼 메모리를 사용하도록 크기를 제한하는 대수(large number)를 지원함을 주목하라.