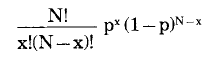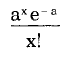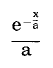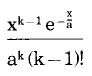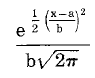Smalltalk80LanguageImplementationKor:Chapter 21
- 제 23 장 확률 분포
확률 분포 프레임워크
시뮬레이션과 같은 애플리케이션에서는 종종 확률 실험의 결과와 관련된 값을 얻고자 할 때가 있다. 이러한 실험에서는 다음을 포함해 여러 질문을 제기할 수 있다.
- 특정 이벤트가 발생할 확률이 얼마나 될까?
- 여러 이벤트 중 하나가 발생할 확률은 얼마나 될까?
- 다음부터 시작해 N회 시도 중에서 최소 한 번의 이벤트 성공할 확률은 얼마나 될까?
- 다음부터 시작해 N회 시도 중에서 몇 번의 이벤트가 성공할까?
- 다음 이벤트 성공까지 몇 회의 시도를 해야 할까?
정의(Definitions)
시뮬레이션 용어에서 "trial"(시도)란 시뮬레이트된 시계의 째깍하는 순간을 나타낸다 (시계가 째깍한다는 것은 상황에 적절한 시간 단위에 따라 초, 분, 시간, 일수, 개월, 또는 연도수를 나타내기도 한다). "Event"(이벤트) 또는 "success"(성공)이란 세차장에 도착한 자동차, 은행에 도착한 손님, 또는 수리점에 도착한 고장난 기계와 같이 업무의 도착을 의미한다.
통계학 영역에서 이벤트가 발생하게 될 확률은 주로 실제 시도를 엄청나게 관찰하여 얻어진다. 가령, 고정된 시간 내에 수리점에 고장난 기계가 도착할 확률을 결정하기 위해서는 오랜 시간 수리점을 관찰해야 할 것이다. 일반적으로 그 시간 동안에는 여러 이벤트가 발생할 수 있다. 이러한 가능한 이벤트 집합을 "sample space"(표본 공간)이라고 부른다. 표본 공간에서 "probability function"(확률 함수)은 표본 공간에 각 이벤트가 있을 때 0과 1 사이 숫자의 연관(association)으로 정의된다. 표본 공간에서 최소 하나의 이벤트가 발생할 확률 또는 가능성을 1로 정의하고, p가 만일 E 이벤트가 발생할 확률이라면 E가 발생하지 않을 확률은 1-p로 정의된다.
표본 공간은 두 가지 유형으로 분류되는데, 바로 이산적 유형과 연속적 유형이다. 표본 공간에 가능한 이벤트의 수가 유한이거나, 양의 정수와 1:1 관계를 가진 이벤트의 수가 무한일 경우 표본 공간은 이산적이다. 예를 들어, 주사위를 던지면 가능한 6가지 결과는 이산적 표본 공간에 해당한다. 반대로 무한한 이벤트의 수가 정렬된 채로 포함된 경우 연속적 표본 공간이 되는데, 1.0과 4.0 사이에 어떠한 수를 예로 들 수 있겠다. 각 유형의 표본 공간에서 확률 함수는 "discrete probability functions"(이산적 확률 함수)와 "continuous probability functions"(연속적 확률 함수)로 적절하게 명명된다.
"Random variable"(무작위 변수)는 표본 공간 내 이벤트에 대해 정의되는 실제 값 함수이다. "이산적" 그리고 "연속적"이라는 형용사는 그 범위의 특징에 따라 무작위 변수에 적용된다. 무작위 변수의 확률 함수를 "probability distribution"(확률 분포)라고 부르는데, 함수 범위 내 값은 무작위 변수에 가능한 값이 발생할 확률에 해당한다. "Density"(밀도)는 무작위 변수에 허용되는 범위로 확률을 할당하는 함수이다. 양의 값만 갖고 적분(integral)이 1이라면 어떤 함수든 "밀도" 함수(이산적 또는 연속적)가 될 수 있다.
시뮬레이션에서 중요한 역할을 하는 또 다른 유용한 함수로 "cumulative distribution function"(누적 분포 함수)가 있다. 이는 무작위 변수의 값이 지정된 범위 내에 있을 확률을 제공한다. 예를 들어, 누적 분포 함수는, "주사위를 던졌을 때 4 이하의 면이 나올 확률은?"이라는 질문에 답한다.
"Mean"(평균)이란 무작위 변수가 취하는 평균 값으로 정의된다. "Variance"(분산)는 분포의 확산에 대한 측정치다. 이는 평균으로부터 편차의 제곱을 평균낸 값이다.
도입 예제(Introductory Examples)
Smalltalk-80 클래스를 상세하게 설명하기 전에 표본 공간의 두 가지 예를 제공하고 있다. 주사위를 던졌을 때 가능한 결과를 표본 공간이라고 가정하자. 표본 공간은 다음으로 구성된다.
event 1:1 is thrown
event 2:2 is thrown
event 3:3 is thrown
event 4:4 is thrown
event 5:5 is thrown
event 6:6 is thrown
그리고 이러한 이산적 확률 분포에서 어떠한 이벤트든 그에 대한 확률 함수는 다음과 같다.
f(event) = 1/6
X가 표본 공간 상에서 무작위 변수라면 X의 확률 분포는 g(X)로 다음과 같다.
g(X=1) = f(event1) = 1/6, ... , g(X=6) = f(event6) = 1/6.
어떤 X 값이든 X의 밀도는 1/6이 된다.
X의 누적 분포 함수는 다음과 같다.
아래를 예로 들 수 있겠다.
c(2,4) = g(X=2) + g(X=3) + g(X=4) = 1/6 + 1/6 + 1/6 = 1/2
연속적 확률 분포의 예로, 요일의 시작 시간이 12:00 a.m. 이고 끝나는 시간이 11:59:59:99... p.m. 인 시각을 표본 공간이라고 치자. 표본 공간은 두 가지 시간 사이의 간격에 해당한다.
확률 함수는 다음과 같고,
eventi < eventj가 충족된다. X의 밀도는 다음과 같다.
g(X = any specified time) = 0
이것이 24시간 시계라고 가정하자. 시계를 쳐다봤을 때 시간이 1:00 p.m.과 3:00 p.m. 사이에 있을 확률은 다음과 같은 누적 분포 함수로 정의되며,
g(X)는 24시간에 걸쳐 균일하다. 따라서 다음과 같이 표현 가능하다.
c(1:00,3:00) = c(1:00, 2:00) + c(2:00, 3:00) = 1/24 + 1/24 = 1/24.
ProbabilityDistribution 클래스
확률 분포에 대한 슈퍼클래스는 분포로부터 하나 또는 그 이상의 무작위 샘플링을 얻고 밀도와 누적 분포 함수를 계산하기 위한 프로토콜을 제공한다. 여기에는 Random 클래스의 인스턴스인 클래스 변수 U가 포함되어 있다. Random 클래스는 간격에 걸쳐 [0,1] 균일한 확률 분포의 값을 얻는 간단한 방법을 제공한다.
Random 클래스와 마찬가지로 ProbabilityDistribution은 알고리즘적으로 생성되는 요소로 접근하는 Stream이다. 무작위 표본이 필요할 때마다 분포로 next 메시지가 전송된다. ProbabilityDistribution은 인자 var가 0과 1 사이의 무작위 숫자에 해당하는 inverseDistribution: var 메시지의 결과를 리턴함으로써 next를 구현한다. ProbabilityDistribution의 서브클래스는 표본 공간에 [0,1]을 매핑하기 위해 inverseDistribution: 을 구현해야 하는데, 그렇지 않으면 next의 정의를 오버라이드해야 한다. next: 메시지는 슈퍼클래스 Stream에서 상속된다.
| 클래스명 | ProbabilityDistribution |
| 슈퍼클래스 | Stream |
| 클래스 변수명 | U |
| 클래스 메서드 | class initialization
initialize
"Uniformly distributed random numbers in the range [0,1]."
U ← Random new
instance creation
new
↑self basicNew
|
| 인스턴스 메서드 | random sampling
next
"This is a general random number generation method for any probability law; use the (0, 1) uniformly distributed random variable U as the value of the law's distribution function. Obtain the next random value and then solve for the inverse. The inverse solution is defined by the subclass."
↑self inverseDistribution: U next
probability functions
density: x
"This is the density function."
self subclassResponsibility
distribution: aCollection
"This is the cumulative distribution function. The argument is a range of contiguous values of the random variable. The distribution is mathematically the area under the probability curve within the specified interval."
self subclassResponsibility
private
inverseDistribution: x
self subclassResponsibility
computeSample: m outOf: n
"Compute the number of ways one can draw a sample without replacement of size m from a set of size n."
m > n ifTrue: [↑0.0].
↑n factorial / (n-m) factorial
|
클래스 변수 U를 초기화하기 위해서는 아래 표현식을 평가한다.
ProbabilityDistribution initialize
크기 n의 집합으로부터 크기 m을 대체하지 않고 표본을 그릴 수 있는 방법의 개수를 계산하면 아래 서브클래스 구현들이 공유하는 유용한 메서드를 확인할 수 있을 것이다.
DiscreteProbability 클래스
두 가지 유형, 이산적 그리고 연속적 확률 분포는 ProbabilityDistribution 클래스의 서브클래스로 명시되며, 각각은 밀도 함수에 의존하는 누적 분포 함수의 구현을 제공한다. 이러한 구현에서는 서브클래스에 밀도 함수가 제공될 것이라고 가정한다.
| 클래스명 | DiscreteProbability |
| 슈퍼클래스 | ProbabilityDistribution |
| 인스턴스 메서드 | probability functions
distribution: aCollection
"Answer the sum of the discrete values of the density function for each element in the collection."
| t |
t ← 0.0.
aCollection do: [ :i | t ← t + (self density: i)].
↑t
|
ContinuousProbability 클래스
| 클래스명 | ContinuousProbability |
| 슈퍼클래스 | ProbabilityDistribution |
| 인스턴스 메서드 | probability functions
distribution: aCollection
"This is a slow and dirty trapezoidal integration to determine the area under the probability function curve y=density(x) for x in the specified collection. The method assumes that the collection contains numerically-ordered elements."
| t aStream x1 x2 y1 y2 |
t ← 0.0.
aStream ← ReadStream on: aCollection.
x2 ← aStream next.
y2 ← self density: x2.
[x1 ← x2. x2 ← aStream next]
whileTrue:
[y1 ← y2.
y2 ← self density: x2.
t ← t + ((x2-x1)*(y2+y1))].
↑t*0.5
|
다양한 유형의 확률 분포를 DiscreteProbability 또는 ContinuousProbability 클래스의 서브클래스로 구현하기 위해서는 밀도 함수와 역 분포 함수 (또는 next에 대한 다른 응답) 모두 구현되어야 한다.
이산적 확률 분포(Discrete Probability Distributions)
이산적 확률 분포의 예로 20명의 학생으로 구성된 학급의 학생 키를 재고 키가 똑같은 학생의 빈도를 나타내는 표를 작성해보자 (키는 인치로 표현). 표는 아래와 같은 모양을 할 것이다.
| 측정된 키 | 학생 수 |
| 60" | 3 |
| 62" | 2 |
| 64" | 4 |
| 66" | 3 |
| 68" | 5 |
| 70" | 3 |
이러한 정보가 주어지면 "키가 5'4" 인 학생을 무작위로 선택할 확률은 무엇일까?"라는 질문을 할 수 있다. 이 질문은 관찰된 정보와 연관된 이산 확률의 밀도 함수를 계산하여 답한다. 특히 아래의 표와 관련된 밀도 함수를 정의할 수 있겠다.
| 높이 | 밀도 |
| 60" | 3/20 |
| 62" | 2/20 |
| 64" | 4/20 |
| 66" | 3/20 |
| 68" | 5/20 |
| 70" | 3/20 |
DiscreteProbability의 서브클래스를 SampleSpace란 이름으로 정의한다고 가정하고 SampleSpace의 인스턴스 변수 값으로 위의 표를 제공하자. density: x 메시지에 대한 응답은 표에 x와 연관된 값이 되고 (이번 예제에서 x의 값은 학생들의 키 중 하나가 되겠다), 표에 제시되지 않은 x의 밀도 값은 0이 된다. 컬렉션의 각 요소의 샘플링 확률은 동일하며, 밀도 함수는 컬렉션 크기의 역수이다. 데이터 요소가 여러 번 발생할 수 있으므로 확률은 각 발생에 대한 확률을 모두 합한 값이 되어야 한다. 누적 분포 함수의 구현은 슈퍼클래스로부터 상속된다.
| 클래스명 | SampleSpace |
| 슈퍼클래스 | DiscreteProbability |
| 인스턴스 변수명 | data |
| 클래스 메서드 | instance creation
data: aCollection
↑self new setData: aCollection
|
| 인스턴스 메서드 | probability functions
density: x
"x must be in the sample space; the probability must sum over all occurrences of x in the sample space"
(data includes: x)
ifTrue: [↑(data occurrencesOf: x) / data size]
ifFalse: [↑0]
private
inverseDistribution: x
↑data at: (x*data size) truncated + 1
setData: aCollection
data ← aCollection
|
heights가 SampleSpace의 인스턴스라고 가정하자. 데이터는 표본에서 각 학생의 키에 해당하는 요소 20로 된 배열이다.
heights ← SampleSpace data: #(60 60 60 62 62 64 64 64 64 66 66 66 68 68 68 68 68 70 70 70)
그리고 나서 키가 64인 학생을 무작위로 선정할 확률, 또는 키가 60" 과 64" 사이의 학생을 무작위로 선정할 확률에 대한 질문을 heights에게 한다. 첫 번째 질문에 대한 답은 밀도 함수, 즉 density: 64 메시지에 대한 응답이 되겠다. 두 번째 질문에 대한 답은 누적 분포 함수, 즉 distribution: (60 to: 64 by: 2) 메시지에 대한 응답이 된다.
SampleSpace는 여러 면에서 이산적 균일 분포와 닮았다. 대체적으로 이산적 균일 분포는 한정된 값의 범위에서 정의된다. 예를 들어 주사위의 면을 나타내는 6개의 값, 1, 2, 3, 4, 5, 6에 대해 균일 분포를 명시할 수 있겠다. 상수 1/6과 같이 밀도 함수는 주사위가 "fair"(공평한)하여 각 면이 선택될 확률이 동일함을 나타낸다.
우리는 시뮬레이션 연구에서 유용한 네 가지 유형의 이산적 확률 분포를 정의할 것이다. 이는 Bernoulli, Binomial, Geometric, Poisson이다. 베르누이 분포는 “다음 시도에서 성공이 발생할 것인가?”라는 질문에 답을 한다. 이항 분포는 N의 반복되고 독립적인 베르누이 분포를 나타내는데, 여기서 N은 1보다 크거나 같다. 이는 N회 시도 중 몇 번 성공하는지에 대한 질문에 답한다. 약간 다른 관점을 취하는 기하 분포는 처음으로 성공하기 전에 반복적이고 독립적인 베르누이 시도가 몇 회 필요한지에 대한 질문에 답한다. 포아송 분포는 특정 기간 동안 얼마나 많은 이벤트가 발생하는지에 대한 질문에 답을 한다. 특히 포아송 분포는 특정 기간 동안 0보다 크거나 동일한 K 이벤트가 발생할 확률을 결정한다.
베르누이 분포(The Bernoulli Distribution)
베르누이 분포는 발생 확률이 주어진 두 가지 가능성에 대한 표본 공간의 경우에 사용된다. 두 가지 가능성으로 구성된 표본 공간의 예로는 다음을 들 수 있다.
- 주사위 던지기에서 “방금 4를 던졌는가?”라고 질문한다. 주사위가 공평하다면 성공 확률은 1/6, 실패 확률은 5/6.
- 동전을 던지고 “방금 앞면이 나왔는가?”라고 질문한다. 동전이 공평하다면 성공 확률은 ½, 실패 확률도 ½.
- 플레잉 카드 돌리기에서 “하트 퀸을 돌리고 있는가?”라고 질문한다. 카드 덱이 표준이라면 성공 확률은 1/52, 실패 확률은 51/52.
Bernoulli 클래스의 명세에 따라 아래의 형태로 된 표현식을 이용해 베르누이 분포를 생성한다.
Bernoulli parameter: 0.17
이번 예제에서 우리는 성공 확률이 0.17인 베르누이 분포를 생성하였다. 성공 확률은 베르누이 분포의 평균이라고 부르기도 한다.
베르누이 분포의 매개변수 prob은 두 가지 가능한 결과 중 하나가 발생할 확률을 의미한다. 이러한 결과를 성공적 결과라고 부른다. 매개변수 prob은 0.0과 1.0 사이의 숫자이다. 밀도 함수는 두 가지 가능한 결과, 1 또는 0을 매개변수 prob 또는 그 역(inverse)으로 매핑한다. 누적 분포는 슈퍼클래스로부터 상속되며, prob 또는 1 값만 리턴할 수 있다.
| 클래스명 | Bernoulli |
| 슈퍼클래스 | DiscreteProbability |
| 인스턴스 변수명 | prob |
| 클래스 메서드 | instance creation
parameter: aNumber
(aNumber between: 0.0 and: 1.0)
ifTrue:[↑self new setParameter: aNumber]
ifFalse:[self error: 'The probability must be between 0.0 and 1.0']
|
| 인스턴스 메서드 | accessing
mean
↑prob
variance
↑prob * (1.0 - prob)
probability functions
density: x
"let 1 denote success"
x = 1 ifTrue: [↑prob].
"let 0 denote failure"
x = 0 ifTrue: [↑1.0 - prob].
self error: 'outcomes of a Bernoulli can only be 1 or 0'
private
inverseDistribution: x
"Depending on the random variable x, the random sample is 1 or 0, denoting success or failure of the Bernoulli trial."
x < = prob
ifTrue: [↑1]
ifFalse: [↑0]
setParameter: aNumber
prob ← aNumber
|
카드 게임을 하던 중간에 어떤 단계에서 첫 번째로 뽑는 카드가 에이스인지 확인하길 원한다고 가정해보자. 그렇다면 가능한 (무작위로 결정된) 응답은 4/52 평균으로 된 베르누이 분포에서 샘플링을 통해 얻을 수 있다.
(Bernoulli parameter: 4/52) next
next 메시지에 대한 응답이 어떻게 실행되는지 확인해보자.
단항 메시지 next와 연관된 메서드는 ProbabilityDistribution 클래스의 메서드 사전에서 찾을 수 있다. 메서드는 self inverseDistribution: U next 표현식의 값을 리턴한다. 즉, inverseDistribution: 의 인자가 되기 위해 0과 1 사이에 균일하게 분포된 숫자를 (U next) 얻는다는 말이다. inverseDistribution: 선택자와 연관된 메서드는 Bernoulli 클래스의 메서드 사전에서 찾을 수 있다. 이는 누적 분포 함수의 prob 값으로부터 x 값으로 매핑하는 역 분포 함수로, prob은 무작위 변수가 x보다 작거나 같을 확률에 해당한다. 베르누이 분포에서 x는 두 가지 값 중 하나여야 하는데, 이는 정수 1과 0로 표기된다.
이항 분포(The Binomial Distribution)
시뮬레이션에서 우리는 이벤트가 발생하는지, 가령 곧이어 차가 도착할 것인지 아니면 오늘 기계가 고장날 것인지를 알려줄 때 베르누이 분포를 사용한다. 이항 분포는 N회의 시도에서 성공 횟수가 얼마나 발생했는지 답해준다. 베르누이 분포의 밀도 함수는 두 이벤트 중 하나가 발생할 확률을 알려준다. 반대로 이항 분포의 밀도 함수는 다음 N회 시도에서 x가 성공할 확률은 무엇인지에 대한 질문에 답한다.
이항 분포는 N회의 반복된 독립적 베르누이 시도를 나타낸다. 이는 N=1에 대한 베르누이와 동일하다. Bernoulli 클래스의 서브클래스인 Binomial 클래스의 설명에서 추가 인스턴스 변수인 N은 시도 횟수를 나타낸다. 즉, Binomial의 인스턴스가 주어졌을 때 next 메시지에 대한 응답은 N회 시도에 성공 횟수가 얼마나 되는지에 대한 질문에 답을 제공한다.
이항에 대한 확률 함수는 다음과 같은데,
x는 성공 횟수, p는 각 시도마다 성공의 확률을 나타낸다. "!" 표시는 수학적 계승 연산을 나타낸다. 첫 항은 N회 시도에서 x회 성공을 얻는 방법의 수에서 x 회 시도 중 x회 성공을 얻는 방법의 수를 나누어 계산된다. 따라서 아래 주어진 구현은 ProbabilityDistribution 슈퍼클래스에 제공된 computeSample: a outOf: b 메서드를 사용한다.
| 클래스명 | Binomial |
| 슈퍼클래스 | Bernoulli |
| 인스턴스 변수명 | N |
| 클래스 메서드 | instance creation
events: n mean: m
n truncated < = 0 ifTrue: [self error: 'number of events must be > 0'].
↑self new events: n mean: m
|
| 인스턴스 메서드 | random sampling
next
| t |
"A surefire but slow method is to sample a Bernoulli N times. Since the Bernoulli returns 0 or 1, the sum will be between 0 and N."
t ← 0.
N timesRepeat: [t ← t + super next].
↑t
probability functions
density: x
(x between: 0 and: N)
ifTrue: [↑((self computeSample: x outOf:N) / (self computeSample: x outOf: x)) * (prob raisedTo: x) * ((1.0 - prob) raisedTo: N - x)]
ifFalse: [↑0.0]
private
events: n mean: m
N ← n truncated.
self setParameter: m/N
"setParameter: is implemented in my superclass"
|
동전 던저기를 예로 들어보자. 동전을 5회 던졌을 때 앞면이 나올 확률은 0.5이면, 매개변수가 0.5인 베르누이 분포는 한 번의 시도, 가령 한 번의 동전 던지기를 나타낸다.
sampleA ← Bernoulli parameter: 0.5
아래 표현식의 결과는
sampleA next
1 또는 0으로, '방금 앞면이 나왔는가?'라는 질문에 대한 답이 된다.
대신 다음을 생성했다고 가정하자.
sampleB ← Binomial events: 5 mean: 2.5
다음의 결과는
sampleB next
0부터 5 사이의 숫자로, '5번 시도에서 앞면이 몇 번 나왔는가?'라는 질문에 답이 된다. 아래의 메시지는
sampleB density: 3
0과 1 사이의 숫자로, '5번 시도 중에 앞면이 3번 나올 확률은 무엇인가?'란 질문에 답을 한다.
기하 분포(The Geometric Distribution)
첫 번째 성공을 하기 전까지 얼마나 많이 반복된 독립적 베르누이 시도가 필요한지에 대한 답을 원한다고 가정하자. 베르누이 분포에 대한 이러한 새로운 관점이 바로 기하 분포이다. 베르누이 및 이항 분포와 마찬가지로 성공 확률은 0.0과 1.0 사이에 있고, 기하의 평균은 성공 확률의 역수이다. 따라서 아래와 같이 기하 분포를 생성한다면,
Geometric mean: 5
평균은 5가 되고 성공 확률은 1/5이 된다. 평균은 0보다 크거나 같아야 한다.
기하 분포는 베르누이 또는 이항 분포보다 이벤트 구동 시뮬레이션 디자인에 더 적합하다. 다음 20초 이내에 몇 대의 차가 도착할 것인지 (이항 질문) 질문하는 대신 기하 분포는 다음 차가 도착하기까지 몇 초가 남았는지를 질문한다. 이벤트 구동 시뮬레이션에서 (시뮬레이트된) 시계는 다음 이벤트의 시간으로 건너뛴다. 기하 분포를 이용하면 다음 이벤트가 언제 발생할 것인지 결정하고 그에 따라 시계를 설정한 다음 이벤트를 실행하여 실제 시간을 엄청나게 “절약”할 잠재력을 지닌다.
다음의 확률 분포 함수에서
x는 필요한 시도 횟수이고, p는 한 번의 시도만에 성공할 확률이다.
| 클래스명 | Geometric |
| 슈퍼클래스 | Bernoulli |
| 클래스 메서드 | instance creation
mean: m
↑self parameter: 1/m
"Note that the message parameter: is implemented in the superclass"
|
| 인스턴스 메서드 | accessing
mean
↑1.0 / prob
variance
↑(1.0 - prob) / prob squared
probability functions
density: x
x > 0 ifTrue: [↑prob * ((1.0 - prob) raisedTo: x - 1)]
ifFalse: [↑0.0]
private
inverseDistribution: x
"Method is from Knuth, Vol. 2, pp. 116-117"
↑(x In / (1.0 - prob) in) ceiling
|
매분 선착장에 평균적으로 두 대의 자동차가 도착한다고 가정하자. 이러한 통계 정보는 아래와 같이 표현할 수 있다.
sample ← Geometric mean: 2/60
밀도 함수를 이용해, "다음 성공까지 N회의 시도가 이루어질 확률은 무엇인가?"라는 질문에 답을 할 수 있다. 질문의 예를 들자면, "다음 자동차가 도착하기까지 30초가 걸릴 확률은 무엇인가?"라는 질문이 있겠다.
sample density: 30
누적 분포 함수를 이용하면, 30초에서 40초 사이에 다음 자동차가 도착했는지에 대한 질문에도 답을 할 수 있다.
sample distribution: (30 to: 40)
포아송 분포(The Poisson Distribution)
단위 시간(또는 공간 간격)에서 이벤트가 몇 번 발생했는지 질문하길 원한다고 가정하자. 이항 분포에서는 두 개의 독립된 이벤트의 발생을 고려하는데, 가령 카드 덱에서 하트 킹 또는 스페이드 킹을 뽑는 경우를 예로 들 수 있겠다. 하지만 임의의 시간 또는 공간 시점에서 무작위 이벤트가 발생하기도 한다. 이러한 이벤트들은 시도의 결과로 발생하는 것이 아니다. 이런 상황에서는 일어나거나 일어나지 않는 이벤트의 확률을 고려하는 것이 의미가 없다. 선착장에 몇 대의 차가 도착하지 않았는지, 혹은 공항에 몇 대의 항공기가 착륙하지 않았는지를 질문하는 이는 없을 것이며, 다음 시간 단위 내에 선착장에 몇 대의 차가 도착했고 공항에 몇 대의 항공기가 착륙했는지가 올바른 질문이 되겠다.
시뮬레이션에서 포아송 분포는 서비스에 대한 손님의 잠재적 요구, 가령 출납원, 판매원, 기술요원 또는 Xerox 복사기를 표본화할 때 유용하다. 경험에 따르면 서비스가 제공되는 속도는 종종 포아송 확률법칙과 비슷하다.
포아송 법칙은 단위 시간당 발생의 평균 속도가 변수 mu일 때 단위 시간 간격에서 x 이벤트가 정확히 몇 번 발생하는지 확률을 설명한다. 시간 간격이 dt일 때 확률은 mu*dt이고, mu는 0.0보다 커야 한다.
확률 함수는 다음과 같으며,
여기서 a는 평균 속도(또는 mu), e는 자연로그의 밑, x는 발생 횟수, !는 계승의 표시다.
| 클래스명 | Poisson |
| 슈퍼클래스 | DiscreteProbability |
| 인스턴스 변수명 | mu |
| 클래스 메서드 | instance creation
mean: p
"p is the average number of events happening per unit interval."
p > 0.0
ifTrue: [↑self new setMean: p]
ifFalse: [self error: 'mean must be greater than 0.0']
|
| 인스턴스 메서드 | accessing
mean
↑mu
variance
↑mu
random sampling
next
"how many events occur in the next unit interval?"
| p n q |
p ← mu negated exp.
n ← 0.
q ← 1.0.
[q ← q * U next.
q > = p]
whileTrue: [n ← n + 1].
↑n
probability functions
density: x
"the probability that in a unit interval, x events will occur"
x > = 0
ifTrue: [↑((mu raisedTo: x) * (mu negated exp)) / x factorial]
ifFalse: [↑0.0]
private
setMean: p
mu ← p
|
next 메시지에 대한 응답은 "다음 시간 단위 또는 공간 단위에서 이벤트가 몇 번 발생하는가?"란 질문에 답한다. x의 밀도 함수는 어떤 (시간 또는 공간) 단위 간격에서 x 이벤트가 발생하게 될 확률을 결정한다. x의 누적 분포 함수는 단위 간격에서 x 또는 그보다 작은 수의 이벤트가 발생하게 될 확률을 결정한다.
연속적 확률 분포(Continuous Probability Distributions)
연속적 무작위 변수는 간격 또는 간격의 컬렉션에서 어떠한 값이든 가정할 수 있다. 연속적 사례에서는 이산적 사례의 질문과 비슷한 질문을 하고 연속적 확률 분포는 이산적 확률 분포에 대해 더 강한 대응(correspondence)를 보인다. 연속적 확률 분포에 대한 질문의 예로, 어떤 특정 시간에 온도를 측정할 확률은 무엇인지를 들 수 있겠다. 온도는 연속된 척도에서 측정되는 물리적 속성이다.
우리는 연속적 확률 분포의 유형 네 가지를 정의하는데, 바로 균일, 지수, 감마, 정규 분포가 해당된다. 균일 분포는 동일한 가능성을 가진 이벤트 집합이 주어질 때 그 중 어떤 것이 발생하는지에 대한 질문을 한다. 기본이 되는 이벤트가 포아송 분포된 경우 지수 분포를 이용해 첫 번째 (다음) 이벤트가 발생하기까지 얼마나 시간이 남았는지 등의 질문에 답을 할 수 있다. 감마 분포는 N 번째 이벤트가 발생하기까지 얼마나 남았는지의 질문과 관련된다. 정규 또는 가우스 분포는 다른 제한된 형태의 분포의 근사치를 계산하는 데 유용하다. 이는 사용하기가 간단하고, 평균과 관련해 대칭적이며, 두 개의 매개변수인 평균과 분산으로 결정되고, 일상 생활의 이벤트 분포를 반영하기 때문에 통계학에서 매우 중요한 역할을 한다.
균일 분포(The Uniform Distribution)
한정된 표본 공간에서 이산적 요소를 선택하는 관점에서 이미 균일 분포를 살펴보았다. 우리가 질문한 것은, 동일한 가능성의 설명이 주어졌을 때 어떤 것을 선정할까가 된다. 연속적 사례에서는 표본 공간이 시간이나 0과 1 사이 간격처럼 연속적이다. 본문에 제시된 Uniform 클래스는 next 메시지에 대한 응답으로 어떠한 간격 내에서든 무작위 변수를 생성함으로써 Random 클래스의 기능을 확장한다.
| 클래스명 | Uniform |
| 슈퍼클래스 | ContinuousProbability |
| 인스턴스 변수명 | startNumber stopNumber |
| 클래스 메서드 | instance creation
from: begin to: end
begin > end
ifTrue: [self error: 'illegal interval']
ifFalse: [↑self new setStart: begin toEnd: end]
|
| 인스턴스 메서드 | accessing
mean
↑(startNumber + stopNumber)/2
variance
↑(stopNumber - startNumber) squared / 12
probability functions
density: x
(x between: startNumber and: stopNumber)
ifTrue: [↑1.0 / (stopNumber - startNumber)]
ifFalse: [↑0]
private
inverseDistribution: x
"x is a random number between 0 and 1"
↑startNumber + (x * (stopNumber - startNumber))
setStart: begin toEnd: end
startNumber ← begin.
stopNumber ← end
|
지수 분포(The Exponential Distribution)
기본이 되는 이벤트가 포아송 분포되었다고 가정할 때 지수 분포는 다음 이벤트가 발생하기까지 얼마나 남았는지를 결정한다. 각 시간 단위를 순서대로 거치는 대신 시뮬레이트된 시계 설정을 이벤트의 다음 발생으로 건너뛰게 할 수 있다는 점에서 이항 분포보다 기하 분포가 더 적합했던 것처럼 지수 분포는 시뮬레이션 디자인에 있어 포아송 분포보다 더 적합하다고 할 수 있다.
지수를 이용한 샘플링의 예로, 다음 승용차가 언제 도착할 것인지 질문해볼 수 있겠다. x의 목적지 함수는 다음 이벤트가 x 시간 간격 내에 발생할 확률, 가령 지금부터 10분 이내에 다음 승용차가 도착할 확률을 나타낸다.
지수는 주로 시간에 따라 표본의 상태가 악화되는 상황에서 사용되는 것이 보통이다. 예를 들어 지수는 전구 또는 전자 기기의 부품 하나가 x 시간이 지나기 전에 고장날 확률을 결정하는 데 사용된다. 기기의 부품을 오래 사용할수록 작동될 가능성이 낮기 때문에 이러한 상황에서 지수 분포가 유용하다.
포아송의 사례와 마찬가지로 지수 분포의 매개변수 mu는 시간 단위별 이벤트와 관련이 있는데, 지수 분포의 영역은 (이벤트가 아니라) 시간이 된다.
지수 분포에 대한 확률 함수는 다음과 같으며,
여기서 a는 발생 간 평균 속도(mu=1/a)이다.
| 클래스명 | Exponential |
| 슈퍼클래스 | ContinuousProbability |
| 인스턴스 변수명 | mu |
| 클래스 메서드 | instance creation
mean: p
"Since the exponential parameter mu is the same as Poisson mu, if we are given the mean of the exponential, we take reciprocal to get the probability parameter"
↑self parameter: 1.0/p
parameter: p
p > 0.0
ifTrue: [↑self new setParameter: p]
ifFalse: [self error: 'The probability parameter must be greater than 0.0']
|
| 인스턴스 메서드 | accessing
mean
↑1.0/mu
variance
↑1.0/(mu * mu)
probability functions
density: x
x > 0.0
ifTrue: [↑mu * (mu * x) negated exp]
ifFalse: [↑0.0]
distribution: anInterval
anInterval stop < = 0.0
ifTrue: [↑0.0]
ifFalse: [↑1.0 - (mu * anInterval stop) negated exp -
(anInterval start > 0.0
ifTrue: [self distribution: (0.0 to: anInterval start)]
ifFalse: [0.0])]
private
inverseDistribution: x
"implementation according to Knuth, Vol. 2, p. 114"
↑x In negated / mu
setParameter: p
mu ← p
|
감마 분포(The Gamma Distribution)
지수와 관련된 분포로 감마 분포가 있는데, 이는 N 번째 이벤트가 발생하기까지 얼마나 남았는지와 같은 질문에 답한다. 예를 들자면 선착장에 N 번째 승용차가 도착하기까지 시간이 얼마나 남았는지를 표본화할 때 감마 분포를 사용하면 된다. Gamma 클래스의 각 인스턴스는 N 번째 이벤트, 그리고 그 이벤트의 발생 확률을 (Exponential 슈퍼클래스로부터 상속됨) 표현한다. Gamma 클래스에 명시된 변수 N은 양의 정수다.
확률 함수는 다음과 같으며,
k는 0보다 크고 확률 매개변수 mu는 1/a이다. 분모의 두 번째 항 (k-1)!는 k가 0보다 크다고 알려지면 감마 함수가 된다. 아래 제공된 구현은 이러한 가정을 하지 않는다.
| 클래스명 | Gamma |
| 슈퍼클래스 | Exponential |
| 인스턴스 변수명 | N |
| 클래스 메서드 | instance creation
events: k mean : p
k ← k truncated.
k > 0
ifTrue: [↑(self parameter: k/p) setEvents: k]
ifFalse: [self error: 'the number of events must be greater than 0']
|
| 인스턴스 메서드 | accessing
mean
↑super mean * N
variance
↑super variance * N
probability functions
density: x
| t |
x > 0.0
ifTrue: [t ← mu * x.
↑(mu raisedTo: N) / (self gamma: N) * (x raisedTo: N - 1) * t negated exp]
ifFalse: [↑0.0]
private
gamma: n
| t |
t ← n - 1.0.
↑self computeSample: t outOf: t
setEvents: events
N ← events
|
정규 분포(The Normal Distribution)
가우스 분포라고도 불리는 정규 분포는 다른 분포의 근사치를 계산하거나 요약하는 데 유용하다. 정규 분포를 이용하면 성공이 발생하기까지 (이산적 이항 분포와 유사) 얼마나 남았는지 혹은 특정 시간 간격 이내에 얼마나 많은 이벤트가 발생하는지 (포아송 분포와 유사) 등의 질문을 할 수 있다. 또한 이벤트의 수가 너무 클 때는 이항 분포의 근사치를 내고, 평균이 너무 클 때는 포아송의 근사치를 내는 데 사용할 수 있다. 하지만 근사치는 평균에 가까운 영역에서만 정확하며, 꼬리 부분을 향할수록 오차가 커진다.
정규 분포는 중간의 두드러진 값(평균)이 있을 때 사용되고, 값을 얻는 확률은 평균으로부터 벗어나면서 감소된다. x 축에는 가능한 값이 있고 y 축에는 확률이 표시된 곡선을 그리면 곡선은 벨 모양과 같을 것이다. 이러한 벨 모양은 확률이 평균을 기준으로 대칭하고, 표본 공간으로부터 가능한 값은 무한하며 이러한 무한한 값의 모든 확률을 합하면 1이 되어야 한다는 요구사항 때문이다. 정규 분포는 볼 베어링의 크기를 측정할 때처럼 측정치의 확률을 결정 시 유용하다. 측정치는 중간 평균 값에서 약간 벗어나 값이 몰려 있는 형태를 야기하게 될 것이다.
정규 분포의 매개변수는 평균(mu)과 표준 편차(sigma)로 되어 있다. 표준 편차는 0보다 커야 한다. 확률 함수는 아래와 같은데,
a는 매개변수 mu이고, b는 표준 편차 sigma이다.
| 클래스명 | Normal |
| 슈퍼클래스 | ContinuousProbability |
| 인스턴스 변수명 | mu sigma |
| 클래스 메서드 | instance creation
mean: a deviation: b
b > 0.0
ifTrue: [↑self new setMean: a standardDeviation: b]
ifFalse: [self error: 'standard deviation must be greater than 0.0']
|
| 인스턴스 메서드 | accessing
mean
↑mu
variance
↑sigma squared
random sampling
next
"Polar method for normal deviates, Knuth vol. 2, pp. 104, 113"
| v1 v2 s rand u |
rand ← Uniform from: -1.0 to: 1.0.
[v1 ← rand next.
v2 ← rand next.
s ← v1 squared + v2 squared.
s > = 1] whileTrue.
u ← (-2.0 * s In / s) sqrt.
↑mu + (sigma * v1 * u)
probability functions
density: x
| twoPi t |
twoPi ← 2 * 3.1415926536.
t ← x - mu / sigma.
↑(-0.5 * t squared) exp / (sigma * twoPi sqrt)
private
setMean: m standardDeviation: s
mu ← m.
sigma ← s
|
다음 장부터는 이산적이고 이벤트 구동 시뮬레이션을 지원하는 클래스 설명을 정의하고 사용 예를 제공하고자 한다. 시뮬레이션 예제에서는 본장에서 정의한 확률 분포를 사용할 것이다.