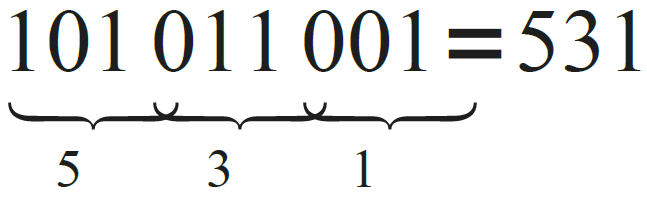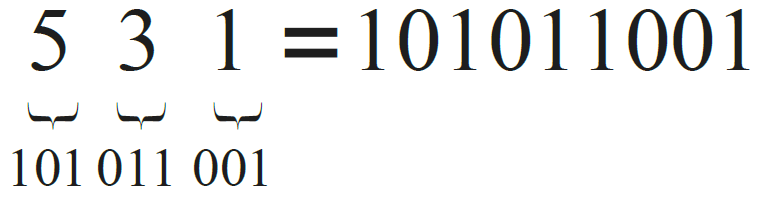ComputerProgrammingwithGNUSmalltalk:1.3
숫자 체계
이전에 컴퓨터 하드웨어가 0과 1만을 이해할 수 있다고 간단히 설명하였습니다. 이제는 왜 그러한지, 조금 더 자세한 이유를 설명할 것입니다. 오늘날 컴퓨터에서 일반적으로 사용하는 하드웨어는 하드웨어의 디자인 때문에 두 가지 상태만을 알아볼 수 있습니다. 예를 들어 이 두가지 상태를 on과 off로 부를 수 있습니다. 따라서 인간은 두 가지 기로호만 세상을 표현할 수 있는 방법이 필요했습니다. 두 기호로 수학을 기술하는 방법은 이미 구현되어 있어서, 두 기호를 다른 것으로 나타내는 것만이 필요했습니다. 예를 들어, 컴퓨터 세계에서 냉장고를 어떻게 나타낼 수 있겠습니까? 우리는 몇몇 문자열의 집합으로 표현할 수 있습니다. 그럼 어떻게 두 가지 기호를 가지고 문자열들을 표현할 수 있겠습니까? 인간은 두 가지 기호로 문자열을 표현하는 방법을 개발했고, 이 내용은 파일 형식 주제에서 보여줄 것입니다. 몇몇 상태들을 표현할 수 있지만, 이 상태들을 변경할 필요도 있을 것입니다. 이러한 것은 몇몇 기본 명령어를 정의하고 기본 내용 위에 더욱 복잡한 것을 구축하는 것으로 달성할 수 있습니다. 이 방법은 기계어로부터 어셈블리 언어까지 그리고 우리가 이 장 이전에서 언급한 더 고수준의 언어까지 통하는 방법입니다.
비록 컴퓨터에서 어떤 일이 일어나는지에 대해 설명하려 했지만, 이 부분에 대한 자세한 내용은 다루지 않을 것입니다. 오로지 두 기호를 이용하여 세계를 어떻게 생성하는지 스스로 상상할 수 있을 것입니다. 이러한 것은 컴퓨터를 이해하는 데에 실제 도움이 될 것이며, 여러분들에게 흥미로운 연습이 될 것입니다. 여러분 스스로 상상해 본 뒤, 어셈블리 언어가 이 문제를 어떻게 해결했는지 보시기 바랍니다. 물론 초보자들에게 아주 어려울 것이기 때문에, 이 장의 글을 다 읽고 난 후에 보길 권장합니다.
이제 우리는 두 기호로 이루어진 세계에서의 수학적 부분에 대해 얘기할 것입니다. 비록 자세히 설명한다 하더라도, 수학 개념으로 여러분을 지루하게 만들지는 않을 것입니다. 앞으로 나올 내용을 깊이 이해하기 위해, 미리 선형대수 책을 보는 것도 나쁘지 않습니다.
십진수 숫자 체계
우리는 매일 실생활에서 (0,1,2,3,4,5,6,7,8 그리고 9까지) 10개의 기호로 표현하는 숫자들을 사용합니다. 왜 9개나 11개가 아닌 10개였을까요? 숫자를 표현하는 데 10개의 기호를 사용하도록 세상이 창조되었을까요? 물론 아닙니다. 우리는 우리가 원하는 만큼의 많은 기호로 숫자를 표현할 수 있습니다. 10개의 기호를 사용하는 이유는 우리가 그렇게 써왔기 때문입니다. 최초의 인도인들이 사용한 방식이 세계로 전파되어서 그렇습니다. 왜 인도인들은 10개의 기호로 숫자를 표현했을까요? 사람의 손가락이 10개였기 때문입니다.
2진수 숫자 체계
수학에선 우리가 숫자를 표현할 때, 원하는 만큼의 기호를 이용하여 표현할 수 있도록 허용합니다. 그러나 컴퓨터에서는 구조상 두 가지 기호만을 사용하기 때문에, 컴퓨터의 작업을 위해서는 2진수 체계가 적합한 것입니다. 2진수는 보통 바이너리 숫자binary number라고 불립니다. 보통 두 기호를 0과 1로 표현하지만, 우리가 원하는 다른 기호를 선택할 수도 있습니다.
일단 x진수의 숫자(여기서 x는 자연수)를 어떻게 십진수로 변환할 수 있는지를 보여드리겠습니다. x진수로 숫자를 쓸 때, 여러분은 각 자리의 해당 자릿값을 쓰고, 진수만큼의 배에 해당하는 경우, 윗 자리에 자릿수를 씁니다. 표현은 혼동되지만, 맞죠? 예를 들어봅시다. 10진수로 345를 예로 들어보지요. 이 값은 다음과 같이 구할 수 있습니다.
따라서 2진수 값의 같은 수인 101011001에 대해서도 다음과 같이 쓸 수 있습니다.
이것은 어떻게 x진수를 10진수로 변환할 수 있는지 보여주는 예입니다. 이제 10진수의 수를 어떻게 2진수로 변환하는지를 보여드리겠습니다. 345를 2진수로 표현하려 한다고 가정해봅시다. 우리가 할 일은 345를 2진수로 표현할 수 있을 때까지 계속 나누는 것입니다. 그 다음, 최종결과값과 나눗셈에서 나온 나머지 값을 오른쪽에서부터 왼쪽으로 하나씩 써두는 것입니다. 이 과정을 보여드리겠습니다.
345 / 2 = 172 (remainder 1)
172 / 2 = 86 (remainder 0)
86 / 2 = 43 (remainder 0)
43 / 2 = 21 (remainder 1)
21 / 2 = 10 (remainder 1)
10 / 2 = 5 (remainder 0)
5 / 2 = 2 (remainder 1)
2 / 2 = 1 (remainder 0)
마지막 나눗셈 결과 값과, 나눗셈의 나머지 값을 (방정식에서 굵게 표시된 숫자들을) 차례대로 오른쪽에서부터 왼쪽으로 써 나가면, 101011001 이라는 숫자를 얻을 수 있으며, 처음 가정했던 수의 2진수 값과 같습니다.
컴퓨터 용어에선 2진수 한 자리를 비트라고 하며, 8개의 비트를 바이트라고 부릅니다.
8진수 숫자 체계
때때로 우리는 바이너리 대신, 8진수로 표현한 숫자들을 쓸 때가 있습니다. 이유는 8진수가 더 짧게 표현되며, 8진수와 2진수의 변환이 쉽기 때문입니다. 이 또한 배우는 것이 역사적으로 도움이 된다는 것을 알 수 있습니다.
8진수를 표현하기 위해, 0부터 7까지의 숫자를 사용할 것입니다. 이진수의 숫자를 8진수로 변환해야 할 텐데, 이진수 오른쪽 끝부터 세 자리씩 묶어서, 각 묶음의 값을 8진수의 값으로 변환하면 변환이 끝납니다. 예를 들어, 바이너리로 쓰여진 101011001값을 8진수로 표현하는 것을 보면 다음과 같습니다.
만약 숫자가 세 개씩 나뉘어 떨어지지 않는다면, 앞에 0을 추가하여 남은 자릿수를 채워넣으면 됩니다.
역으로, 8진수의 수를 바이너리로 변환하는 것 또한 바로 가능합니다. 여러분은 8진수의 각 자릿수 값을 이진수로 변환하여 바로 붙이면 됩니다. 예를 들어, 8진수 531은 2진수로 다음과 같이 표현합니다.
왜 이러한 변환이 항상 옳은지 설명할 수 있습니까?
16진수 숫자 체계
이제 처음으로, 보통은 상상하기 힘든 진수, 16진수에 대해 알아볼 것입니다. 16진수란 숫자를 쓰는데 16개의 기호를 쓴다는 것을 의미합니다. 그러나 아라비아 숫자 기호는 10개 밖에 없습니다. 그럼 어떻게 해야 할까요? 수학에선 10개 외의 나머지 기호를 쓸 수 있도록 허용되어 있습니다. 보통 라틴 알파벳 문자, A, B, C, D, E, F 를 따와서 각각 10, 11, 12, 13, 14, 15의 값으로 사용합니다.
이 경우 우리가 “12개의 초콜릿이 내 앞에 있다.”고 표현하는 대신, 16진수를 사용하는 행성에서 온 외계인은 매일 “C 개의 초콜릿이 내 앞에 있다.”고 표현할 수 있으며, 전반적으로 그렇게 사용할 것이란 얘기입니다.
2진수에서 16진수로 변환을 하는 것은 2진수 네 자리를 기준으로 하는 것을 제외하면 2진수와 8진수 사이를 변환하는 것과 매우 흡사합니다.